Exercice 6: ★ ★ ☆ ☆ ☆

Étudier les limites de \( f \) aux bornes de son ensemble de définition.
a) \( f(x) = \ln(3 - 4x) \), \( I = ]-\infty ; \frac{3}{4}[\)
b) \( f(x) = \ln\left(\frac{2 - x}{x + 1}\right) \), \( I = ]-1 ; 2[\)

Exercice 7: ★ ★ ★ ☆ ☆

Soit la fonction \( f \) définie sur \( ]0 ; +\infty[ \) par \( f(x) = (\ln x)^2 - (1 + e)\ln x + e \).

1. Calculer les limites de \( f \) aux bornes de son ensemble de définition.
2. a) Calculer \( f'(x) \) et montrer que \( f'(x) = \frac{{2\ln x - 1 - e}}{{x}} \).
    b) En déduire le tableau de variations de \( f \) sur \( ]0 ; +\infty[ \).
    c) En déduire le nombre d'antécédents de 0 par \( f \).
    d) Retrouver la réponse en résolvant une équation, puis en déduire la valeur exacte du ou des antécédents.

Exercice 8: ★ ★ ★ ☆ ☆

A - On considère la fonction \( g \) définie sur l'intervalle \( ]0 ; +\infty[ \) par \( g(x) = 2x^3 - 1 + 2\ln x \).
    1. Étudier les variations de la fonction \( g \) sur l'intervalle \( ]0 ; +\infty[ \).
    2. Justifier qu'il existe un unique réel \( \alpha \) tel que \( g(\alpha) = 0 \).
    Donner une valeur approchée de \( \alpha \), arrondie au centième.
    3. En déduire le signe de la fonction \( g \) sur l'intervalle \( ]0 ; +\infty[ \).

B - On considère la fonction \( f \) définie sur l'intervalle \( ]0 ; +\infty[ \) par \( f(x) = 2x - \frac{{\ln x}}{{x^2}} \).
    On note \( C \) la courbe représentative de la fonction \( f \) dans le plan, muni d'un repère orthonormal \( (O ; i , j) \).
        1. Déterminer les limites de la fonction \( f \) en 0 et en \( +\infty \).
        2. Étudier la position relative de la courbe \( C \) et de la droite \( \Delta \) d'équation \( y = 2x \).
        3. Justifier que \( f'(x) \) a le même signe que \( g(x) \).
        4. En déduire le tableau de variations de la fonction \( f \).
        5. Tracer la courbe \( C \) dans le repère \( (O ; i , j) \).
    On prendra comme unité :
        • 2 cm sur l'axe des abscisses ;
        • 1 cm sur l'axe des ordonnées.

A - On considère la fonction \(g\) définie sur l'intervalle \(]0 ; +\infty[\) par \(g(x) = 2x^3 - 1 + 2\ln x\).

    1. Étudie des variations de la fonction \(g\) sur l'intervalle \(]0 ; +\infty[\).
       • Calculons la dérivée de \(g\) :
         \[g'(x) = 6x^2 + \frac{2}{x}\]
       • La fonction \(g\) est dérivable sur \(]0 ; +\infty[\) et \(g'(x) > 0\) pour tout \(x > 0\).
       • Donc \(g\) est strictement croissante sur \(]0 ; +\infty[\).

    2. Justifions qu'il existe un unique réel \(\alpha\) tel que \(g(\alpha) = 0\).
       • Comme \(g\) est strictement croissante, elle admet au plus une seule solution \(\alpha\) telle que \(g(\alpha) = 0\).
       • De plus, \(g(0) = -1 < 0\) et \(\lim_{x \to +\infty} g(x) = +\infty\).
       • Donc, il existe bien un unique réel \(\alpha\) tel que \(g(\alpha) = 0\).
       • Une valeur approchée de \(\alpha\) arrondie au centième est \(\alpha \approx 0,63\).

    3. En déduisons le signe de la fonction \(g\) sur l'intervalle \(]0 ; +\infty[\).
       • Comme \(g\) est strictement croissante et \(g(0) < 0\), on a :
         • \(g(x) < 0\) pour \(x \in ]0 ; \alpha[\),
         • \(g(x) = 0\) pour \(x = \alpha\),
         • \(g(x) > 0\) pour \(x \in ]\alpha ; +\infty[\).

B - On considère la fonction \(f\) définie sur l'intervalle \(]0 ; +\infty[\) par \(f(x) = 2x - \frac{\ln x}{x^2}\).

    1. Les limites de la fonction \(f\) en 0 et en \(+\infty\).
       • \(\lim_{x \to 0^+} f(x) = +\infty\)
       • \(\lim_{x \to +\infty} f(x) = +\infty\)

    2. Étudions la position relative de la courbe \(C\) et de la droite \(\Delta\) d'équation \(y = 2x\).
       \(f(x) < 2x\) pour \(x > 0\), donc la courbe \(C\) est en-dessous de la droite \(\Delta\).

    3. Justifions que \(f'(x)\) a le même signe que \(g(x)\).
       • \(f'(x) = 2 - \frac{1 - \ln x}{x^2}\)
       • \(g'(x) = 6x^2 + \frac{2}{x}\)
       • Comme \(6x^2 + \frac{2}{x} > 0\) pour tout \(x > 0\), \(f'(x)\) et \(g(x)\) ont le même signe.

    4. En déduisons le tableau de variations de la fonction \(f\).
       Comme \(f'(x)\) a le même signe que \(g(x)\), et que \(g\) est strictement croissante, \(f\) est strictement croissante sur \(]0 ; +\infty[\).
5. Tracage de la courbe :

Exercice 9: ★ ★ ★ ☆ ☆

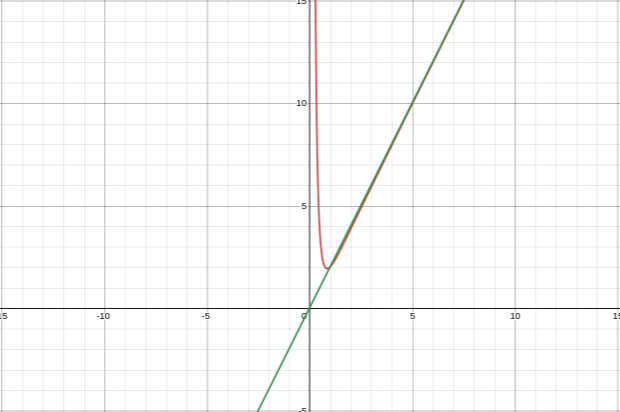
On considère la fonction \( f \) définie sur \( ]0 ; +\infty[ \) par : \[ f(x) = (\ln x)^2 - 2 \ln x \]
On note \( C \) sa courbe représentative dans un repère orthonormé.
1. a) Étudier la limite de \( f \) aux bornes de son ensemble de définition.
    b) En déduire l'existence d'asymptotes pour la courbe \( C \).

2. a) Montrer que \( f'(x) = \frac{{2(\ln x - 1)}}{{x}} \)
    b) En déduire le tableau de variations de \( f \).
3. Résoudre l'équation \( f(x) = 0 \).
4. Construire \( C \) et ses asymptotes.

Exercice 10: ★ ★ ★ ☆ ☆

On considère l'équation \( (E_1) \quad e^x - x^n = 0 \) où \( x \) est un réel strictement positif et \( n \) un entier naturel non nul.
1. Montrer que l'équation \( (E_1) \) est équivalente à l'équation \( (E_2) \quad \ln x - \left(\frac{x}{n}\right) = 0 \).
2. Pour quelles valeurs de \( n \) l'équation \( (E_1) \) a-t-elle deux solutions ?

Exercice 11: ★ ★ ★ ☆ ☆

Sur le graphique ci-dessous, on a tracé, dans le plan muni d'un repère orthonormé \( (O ; i , j) \), la courbe représentative \( C \) d'une fonction \( f \) définie et dérivable sur l'intervalle \( ]0 ; +\infty[ \).

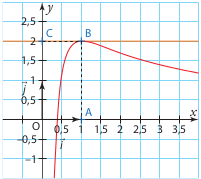
On dispose des informations suivantes :
• Les points A, B et C ont pour coordonnées respectives (1 ; 0), (1 ; 2), (0 ; 2).
• La courbe \( C \) passe par le point B et la droite \((BC)\) est tangente à \( C \) en B.
• Il existe deux réels positifs \( a \) et \( b \) tels que, pour tout réel strictement positif \( x \), \( f(x) = \frac{{(a + b \ln x)}}{x} \).
1. a) En utilisant le graphique, donner les valeurs de \( f(1) \) et \( f'(1) \).
    b) Vérifier que, pour tout réel strictement positif \( x \), \( f'(x) = \frac{{(b - a) - b \ln x}}{{x^2}} \).
    c) En déduire les réels \( a \) et \( b \).
2. a) Justifier que, pour tout réel \( x \) appartenant à l'intervalle \( ]0 ; +\infty[ \), \( f'(x) \) a le même signe que \( -\ln x \).
    b) Déterminer les limites de \( f \) en 0 et en \( +\infty \).
On pourra remarquer que, pour tout réel \( x \) strictement positif, \( f(x) = \frac{2}{x} + \frac{{2 \ln x}}{x} \).
    c) En déduire le tableau de variations de la fonction \( f \).
3. a) Démontrer que l'équation \( f(x) = 1 \) admet une unique solution \( \alpha \) sur l'intervalle \( ]0 ; 1] \).
    b) Par un raisonnement analogue, on démontre qu'il existe un réel \( \beta \) de l'intervalle \( ]1 ; +\infty[ \) tel que \( f(\beta) = 1 \).
Déterminer l'entier \( n \) tel que \( n ﹤ \beta ﹤ n + 1 \).
4. On donne l'algorithme ci-dessous écrit en langage Python :

a) Quel est le rôle de la fonction Python \(f\) ?
b) Quel est le rôle de ce programme ?
c) Quelle instruction Python faudrait-il modifier afin que ce programme affiche les deux bornes d’un encadrement de \(β\) d’amplitude \(10^{–2}\) ?

Exercice 12: ★ ☆ ☆ ☆ ☆

Résoudre dans \(\mathbb{R}\) les équations suivantes en posant \( X = \ln(x) \) ou \( X = e \).
    1. \((\ln(x))^2 - 2\ln(x) - 3 = 0\)
    2. \(4(\ln(x))^2 - \ln(\frac{1}{x} ) - 3 = 0\)
    3. \(4e^{2x} + 7e^x - 2 = 0\)

Exercice 13: ★ ☆ ☆ ☆ ☆

Résoudre dans \(\mathbb{R}\) les équations suivantes.
    1. \(ln(-x) = ln(x^2 - 1) = 0\)
    2. \(ln(2 - e^x) - ln(2e^x - 1) = 0\)
    3. \(ln(4) + ln(x - 1) = 2 ln(x)\)

Exercice 14: ★ ☆ ☆ ☆ ☆

Résoudre dans \(\mathbb{R}\) les inéquations suivantes.
    1. \((e^x - 3)ln(x + 1) < 0\)
    2. \(ln(e^x - 2) < 0\)
    3. \(ln(-x^2 + 4x + 5) < ln(x + 1)\)

Exercice 15: ★ ★ ☆ ☆ ☆

Pour chacune des fonctions \(f\) suivantes définies sur l'ensemble \(E\), étudier les limites de \(f\) aux bornes de \(E\), le sens de variation de \(f\) sur \(E\) et dresser son tableau de variation sur \(E\).
   1. \(f(x)=\frac{x}{ln x}\) et \(E = ]0; 1[\cup]1; +∞[\).
   2. \(f(x)=(ln(x))^2 - ln(x) - 2\) et \(E =]0; +∞[\).

Exercice 16: ★ ★ ☆ ☆ ☆

Soit \((u_n)\) une suite géométrique de raison \(q > 0\) et de premier terme \(u_0 > 0\). On pose \(v_n = ln(u_n)\).
Démontrer que la suite \((v_n)\) est arithmétique.

Exercice 17: ★ ★ ☆ ☆ ☆

Déterminer la valeur exacte du nombre réel :\[A = ln(\frac{1}{2})+ln(\frac{2}{3}) + ln(\frac{3}{4}) + ... + ln(\frac{49}{50})\]

Exercice 18: ★ ★ ☆ ☆ ☆

Soit \(f\) la fonction définie, pour tout réel \(x\), par: \(f(x) = ln(1+e^{-x})\).
Démontrer que, pour tout réel \(x\):\[f(x) = −x+ln(1+e^x)\]

Exercice 19: ★ ★ ☆ ☆ ☆

1. Démontrer que pour tout réel \(x>-1\), on a : \(2ln(x+1)= ln(x^2+2x+1)\).
2. Démontrer que pour tout réel \(x\), on a: \(ln(1+e^{-2x}) = -2x + ln(1+ e^{2x})\).

Exercice 20: ★ ★ ☆ ☆ ☆

1. Démontrer que, pour tous réels \(a\) et \(b\) strictement positifs, \(ln(ab) = ln(a) +ln(b)\).
On pourra exprimer \(e^{ln (ab)}\) et \(e^{ln(a) +ln(b)}\)
2. Soient deux réels \(a\) et \(b\) strictement positifs.
   a. \(p\) étant un entier naturel, rappeler les expressions de \(ln(\frac{1}{a})\), \(ln(\frac{a}{b})\), \(ln(\sqrt{a})\) et \(ln(a^p)\) en fonction de \(ln(a)\) et de \(ln(b)\).
   b. Utiliser la même démarche qu'à la question 1 pour démontrer ces égalités.

Exercice 21: ★ ★ ☆ ☆ ☆

On suppose connu le résultat : pour tous réels \(a\) et \(b\) strictement positifs, \(ln(ab) = ln(a) +ln(b)\) et on se propose de démontrer les propriétés suivantes.
Pour tous réels \(a\) et \(b\) strictement positifs et tout entier relatif \(n\):

(1) \(ln(\frac{1}{a}) = -ln (a)\)
(2) \(ln(\frac{a}{b}) = ln (a) – ln(b)\)
(3) \(ln(\sqrt{a}) = \frac{1}{2}ln(a)\)
(4) \(ln(a^n) = nln(a)\)

1. Écrire \(\frac{1}{a} \times a = 1\) et en déduire la propriété (1).
2. Démontrer alors la propriété (2).
3. Écrire que \(\sqrt{a} \times \sqrt{a} = a\) et en déduire la propriété (3).
4. Démontrer la propriété (4) pour \(n\) entier naturel en utilisant le raisonnement par récurrence.
Pour \(n\) entier strictement négatif, écrire \(a^n = \frac{1}{a^{-n}}\)·

Exercice 22: ★ ★ ☆ ☆ ☆

On donne l'algorithme suivant écrit en langage naturel.

      n ← 1
    Tant que ln(n) ≤ A 
    n ← n+1      

1. Quelle est la valeur de la variable \(n\) à la fin de l'exécution de cet algorithme lorsque \(A = 2\) ?
2. Expliquer pourquoi cet algorithme s'arrête quel que soit le nombre réel \(A\) saisi.

Exercice 23: ★ ★ ☆ ☆ ☆

L'évolution d'une population d'animaux en fonction du temps est modélisée par la fonction \(P\) définie par \(P(t) = 50e^{\frac{t}{2}}\), où \(t\) est exprimé en année.
1. Au bout de combien d'années la population initiale aura-t-elle été multipliée par 2 ?
2. Au bout de combien d'années la population dépassera-t-elle les 10 000 individus ?

Exercice 24: ★ ★ ☆ ☆ ☆

Déterminer le plus petit entier naturel \(n\) tel que:
   a. \(0,99 ≤ 10^{-30}\);
   b. \(1,02^n>10^{2019}\)

Exercice 25: ★ ★ ☆ ☆ ☆

Soit \((u_n)\) la suite géométrique de premier terme \(u_0 = 1\) et de raison \(q = 1,001\).
Déterminer, s'il existe, le plus petit entier naturel \(n\) tel que \(u_n >10 000\).

Exercice 26: ★ ★ ☆ ☆ ☆

En 2019, la population d'un animal en voie d'extinction est estimée à 100 000 individus.
En supposant que, chaque année, cette population diminue de 10%, à partir de quelle année cette population sera-t-elle réduite à moins de 1 000 individus ?

Exercice 27: ★ ★ ☆ ☆ ☆

Alice souhaite placer son argent sur un compte épargne rémunéré à 3% par an.
1. Écrire un algorithme en langage Python permettant de déterminer au bout de combien d'années de placement son capital aura doublé.
2. Exécuter ce script dans un éditeur Python et donner le résultat obtenu.
3. Retrouver le résultat précédent par le calcul.

Exercice 28: ★ ★ ☆ ☆ ☆

Déterminer la limite en \(a\) des fonctions \(f\) et \(g\) suivantes définies sur \(]0; +∞[\).
1. \(f(x)=2(ln(x))^2+3ln(x)+1\), avec \(a = +∞\),
2. \(g(x)=-(ln(x))2 + ln(x)\), avec \(a = 0\).
3. \(h(x)=(e^x-1)(2-ln(x))\), avec \(a = +∞\).
4. \(i(x) = \frac{ln(x) - 1}{x}\), avec \(a = 0\).

Exercice 29: ★ ★ ☆ ☆ ☆

Soit \(f\) la fonction définie sur \(]0; +∞[\) par:
\[f(x)= \frac{ln(x)}{2x+1}\]
1. Déterminer la limite de \(f(x)\) lorsque \(x\) tend vers \(0\).
2. a. Vérifier que, pour tout réel \(x > 0\):
\[f(x)= \frac{ln(x)}{x}(\frac{1}{2+\frac{1}{x}})\]
   b. En déduire la limite de \(f(x)\) lorsque \(x\) tend vers \(+∞\).
3. Interpréter graphiquement les résultats précédents.

Exercice 30: ★ ★ ☆ ☆ ☆

On détermine le \(pH\) d'une solution en mesurant la concentration en ions \(H_3O^+\), par exemple à l'aide d'un pH-mètre.
Le \(pH\) est défini par la relation \(pH = -log[H_3O^+]\), où \([H_3O^+]\) est la concentration en \(mol·L^{-1}\) d'ions \(H_3O^+\) de la solution.

On rappelle que \(log(x) = \frac{ln(x)}{ln(10)}\) pour tout réel \(x>0\).
1. Quel est le \(pH\) d'une solution dont la concentration en ions \(H_3O^+\) est de \(10^{-6,5} mol L^{-1}\) ?
2. Quelle est la concentration en ions \(H_3O^+\) d'une solution de \(pH = 8,4\) ?
3. Si la concentration en ions \(H_3O^+\) d'une solution est multipliée par 10 000, quelle augmentation du pH cela produit-il ?

Exercice 31: ★ ☆ ☆ ☆ ☆

Déterminer les ensembles de définition des fonctions suivantes, définies par :
   a. \(f(x)= ln(3x-7)\);
   b. \(g(x)= ln(-x^2+4x-3)\);
   c. \(h(x)= ln(x)-3ln(2-x)\).

Exercice 32: ★ ☆ ☆ ☆ ☆

Résoudre les équations suivantes après avoir déterminé sur quel ensemble on peut les résoudre.
   1. \(ln(x) = ln(x+2)\)
   2. \(ln(-x+3)= ln(3x+5)\)
   3. \(ln(2x^2+4)= ln(-5x+1)\)
   4. \(ln(x^2) = ln(x)+ ln(6)\)
   5. \(ln(x+1)+ln(x-4)= ln(5)\)
   6. \(2ln(x) = ln(5x-3)\)
   7. \(ln[(x-3)(2x+1)] = ln(4)\)
   8. \(ln(x-3) + ln(2x+1)= 3ln(2)\)

Exercice 33: ★ ☆ ☆ ☆ ☆

Résoudre les inéquations suivantes après avoir déterminé sur quel ensemble on peut les résoudre.
   1. \(ln(3x-4) < 0\)
   2. \(ln(-x+3) ≥ 1\)
   3. \(ln(-x+1) ≤ ln(x)\)
   4. \(ln (3+2x) < ln(x-3)\)

Exercice 34: ★ ☆ ☆ ☆ ☆

Le carbone 14 est un isotope radioactif du carbone permettant de dater les restes d'êtres vivants, comme les squelettes ou les fossiles.
La formule suivante donne l'âge \(T\), en année, d'un échantillon en fonction du pourcentage \(p\) de carbone 14 restant : \(T = 8 264ln(\frac{100}{p})\)
1. Le squelette d'un homme de Néandertal contient 2% du carbone 14 initialement contenu dans ses os.
   Estimer l'âge de ce squelette.
2. La datation au carbone 14 a permis d'estimer l'âge d'une momie à 2 500 ans. Quelle proportion de carbone 14 contient-elle encore ?

Exercice 35: ★ ☆ ☆ ☆ ☆

Soient \(f\) la fonction définie sur l'intervalle \(]-2; 2[\) par \(f(x) = ln(\frac{2+x}{2-x})\) et \(C\) sa courbe représentative dans un repère orthogonal.
   1. Justifier que \(f\) est définie sur \(]-2;2[\).
   2. Montrer que la fonction \(f\) est une fonction impaire. Interpréter graphiquement ce résultat.
   3. Démontrer que la courbe  \(C\) admet deux asymptotes verticales que l'on précisera.
   4. Étudier le sens de variation de la fonction \(f\), puis dresser son tableau de variation.

Exercice 36: ★ ☆ ☆ ☆ ☆

Soit \(f\) la fonction définie sur \(]\frac{1}{2} ; +∞[\) par:
\(f(x) = ln(2x-1)-x + 1\).
1. Déterminer la limite de \(f(x)\) en \(\frac{1}{2}\):
2. Montrer que, pour tout réel \(x>\frac{1}{2}\)
\(f(x)=ln(x)-x+1+ln(2-\frac{1}{x})\).
En déduire la limite de \(f(x)\) en \(+∞\).
3. Démontrer que l'équation \(f(x) = 0\) admet deux solutions distinctes \(\alpha\) et \(\beta\) (\(\alpha<\beta\)).
4. Donner la valeur exacte de \(\alpha\) et un encadrement de \(\beta\) d'amplitude \(10^{-2}\).

Exercice 37: ★ ☆ ☆ ☆ ☆

Soient \(f\) la fonction définie sur \(]0; +∞[\) par:
\[f(x) = x^2ln(x)\]
\(C\) et sa courbe représentative dans un repère orthonormé \((0; \vec{i},\vec{j})\).
1. Démontrer qu'il existe une unique tangente à \(C\) passant par \(O\).
2. Préciser l'équation de cette tangente.

Exercice 38: ★ ☆ ☆ ☆ ☆

Soit \((u_n)\) la suite définie pour tout entier naturel \(n\) non nul par \(u_n = ln(\frac{n}{n+1})\)
1. Montrer que \(u_1+ u_2 + u_3 = -ln(4)\).
2. Soit \(S_n\), la somme définie, pour tout entier naturel \(n\) non nul, par:
\[S_n = u_1+ u2+ ... + u_n = \sum_{k=1}^{n} u_k\]
Exprimer \(S_n\), en fonction de \(n\) et déterminer la limite de \(S_n\) quand \(n\) tend vers \(+∞\).

Exercice 39: ★ ☆ ☆ ☆ ☆

Soit \((u_n)\) la suite définie pour tout entier naturel \(n\) non nul par \(u_n = \frac{e^n}{n}\)

1. Avec la calculatrice, conjecturer le sens de variation et la limite éventuelle de la suite \((u_n)\).
2. Soit \((v_n)\) la suite définie pour tout entier naturel \(n\) non nul par \(v_n = ln(u_n)\).
   a. Montrer que la suite \((v_n)\) est décroissante.
   b. Déterminer la limite de la suite \((v_n)\).
3. Démontrer les conjectures émises à la question 1.

Exercice 40: ★ ☆ ☆ ☆ ☆

Dans une pièce à la température constante de 20 °C, Pablo se prépare une tasse de thé.
À l'instant initial \(t = 0\), la température de son thé est égale à 100 °C. Quatre minutes plus tard, elle est de 80 °C.
On admet que la température du thé \(f(t)\), en °C, est donnée par \(f(t) = Ce^{at} + 20\), où \(t\) désigne le temps en minute et \(a\) et \(C\) sont des constantes réelles. Au-dessus de 50 °C, Pablo trouve que le thé est trop chaud et ne peut pas le boire.
Combien de temps devra-t-il attendre pour déguster son thé ?

Exercice 41: ★ ☆ ☆ ☆ ☆

Soit \(f\) la fonction définie sur \([1; +∞[\) par :
\[f(x)=x-\frac{ln x}{x^2}\]
et soit \(C\) sa courbe représentative dans un repère orthonormé.
1. Soit \(g\) la fonction définie sur \([1; +∞[\) par :
\[g(x) = x^2-1+ln(x)\]
Montrer que la fonction \(g\) est positive sur \([1; +∞[\).
2. a. Montrer que, pour tout \(x\) de \([1; +∞[\):
\[f′(x) = \frac{g(x)}{x}\]
   b. En déduire le sens de variation de \(f\) sur \([1; +∞[\).
3. On note \(D\)la droite d'équation \(y = x\).
Étudier la position relative de la courbe \(C\) par rapport à la droite \(D\).
4. Pour tout entier naturel \(k\) supérieur ou égal à 2, on note respectivement \(M_k\), et \(N_k\), les points d'abscisses \(k\) de \(C\) et de \(D\).
   a. Déterminer la limite de \(M_kN_k\), lorsque \(k\) tend vers \(+∞\).
   b. Écrire un algorithme en langage naturel permettant de déterminer le plus petit entier \(k_0\) supérieur ou égal à 2 tel que la distance \(M_kN_k\) soit inférieure ou égale à \(10^{-2}\)

Exercice 42: ★ ☆ ☆ ☆ ☆

Soit \(f\) la fonction définie sur \(]0; +∞[\) par :
\[f(x) = x^2-2+ ln(x)\]
1. Déterminer les limites de \(f\) aux bornes de son ensemble de définition et étudier son sens de variation.
2. Démontrer que l'équation \(f(x)=0\) admet une unique solution \(\alpha\) dans \(]0; +∞[\).
3. Démontrer que \(ln (\alpha) = 2 - \alpha^2\).
4. Étudier le signe de \(f(x)\) suivant les valeurs de \(x\).
5. On donne la fonction suivante écrite en Python.

            
              1 from math import*
              2
              3 def f(x):
              4     return ***2-2+log(x)
              5
              6 def dichotomie (a,b,p): 
              7     while b-a>10**(-p): 
              8        if f(a)*f((a+b)/2)‹0:
              9           b=(a+b)/2
              10       else:
              11          a=(a+b)/2
              12    return a,b
           
        

Exercice 43: ★ ☆ ☆ ☆ ☆

On considère la fonction \(f\), définie sur \(]0; +∞[\) par : \(f(x)=3x-3xln(x)\).
On note \(C\) sa courbe représentative dans un repère orthonormé et \(T\) la tangente à la courbe \(C\) au point d'abscisse \(1\).
Quelle est la position relative de \(C\) et \(T\) ?

Exercice 44: ★ ☆ ☆ ☆ ☆

Début 2019, une nouvelle application pour smartphone est créée. De nombreuses personnes téléchargent cette application sans nécessairement l'utiliser. Une étude a permis de modéliser l'évolution de la fréquence \(f(t)\) des utilisateurs de cette application parmi ceux qui l'ont téléchargée à l'instant \(t\) (en mois) à partir du \(1^{er}\) septembre 2019 (\(t = 0\) correspond au \(1^{er}\) septembre 2019). On a représenté ci-dessous la fonction \(f\).

1. Déterminer graphiquement:
   a. le pourcentage d'utilisateurs de cette application au \(1^{er}\) janvier 2020 puis au \(1^{er}\) janvier 2021;
   b. l'instant \(t\) auquel plus de la moitié des personnes ayant téléchargé l'application l'utilisent.
2. On admet que l'expression de la fonction \(f\) est de la forme \[f(t)=\frac{1}{1+ae^{bt}}\]
a. Déterminer les valeurs de \(a\) et \(b\).
b. Quelle est la limite de \(f\) en \(+∞\) ?  Interpréter ce résultat.
c. Suivant ce modèle, à partir de quand la fréquence des utilisateurs de cette application dépassera-t-elle \(0,99\) ?

Exercice 45: ★ ☆ ☆ ☆ ☆

Soit la courbe d'équation \(y = e^x\). Pour tout réel \(m\), on note \(D_m\) la droite d'équation \(y = mx\).
1. Dans cette question, on choisit \(m = e\).
Démontrer que la droite \(D_e\) est tangente à la courbe \(C\) en son point d'abscisse 1.
2. À l'aide d'un logiciel de géométrie dynamique, conjecturer, selon les valeurs prises par le réel \(m\), le nombre de points d'intersection de la courbe et de la droite \(D_m\)
3. Démontrer cette conjecture.

Exercice 46: ★ ☆ ☆ ☆ ☆

Soit la courbe d'équation \(y = e^x\). Pour tout réel \(m\), on note \(D_m\) la droite d'équation \(y = mx\).
1. Dans cette question, on choisit \(m = e\).
Démontrer que la droite \(D_e\) est tangente à la courbe \(C\) en son point d'abscisse 1.
2. À l'aide d'un logiciel de géométrie dynamique, conjecturer, selon les valeurs prises par le réel \(m\), le nombre de points d'intersection de la courbe et de la droite \(D_m\)
3. Démontrer cette conjecture.

Exercice: 47: ★ ★ ☆ ☆ ☆

Soit \( f \) la fonction définie sur l'intervalle \( ]1; +\infty[ \) par \[ f(x) = \ln x - \frac{1}{\ln x}. \] On nomme \( (C) \) la courbe représentative de \( f \) et \( (\Gamma) \) la courbe d'équation \( y = \ln x \) dans un repère orthogonal \( (0; \vec{i}, \vec{j}) \).

1. Étudier les variations de la fonction \( f \) et préciser les limites en \( 1 \) et en \( +\infty \).

2. a) Déterminer \( \lim_{x \to +\infty} [f(x) - \ln x] \). Interpréter graphiquement cette limite.
   b) Préciser les positions relatives de \( (C) \) et de \( \Gamma \).

3. On se propose de chercher les tangentes à la courbe \( (C) \) passant par le point \( O \).
   a) Soit \( a \) un réel appartenant à l'intervalle \( ]1; +\infty[ \). Démontrer que la tangente \( T_a \) à \( (C) \) au point d'abscisse \( a \) passe par l'origine du repère si et seulement si \( f(a) - a f'(a) = 0 \).
Soit \( g \) la fonction définie sur l'intervalle \( ]1; +\infty[ \) par \[ g(x) = f(x) - x f'(x). \]
   b) Montrer que sur \( ]1; +\infty[ \), les équations \( g(x) = 0 \) et \( (\ln x)^3 - (\ln x)^2 - \ln x - 1 = 0 \) ont les mêmes solutions.
   c) Après avoir étudié les variations de la fonction \( u \) définie sur \( \mathbb{R} \) par \[ u(t) = t^3 - t^2 - t - 1, \] montrer que la fonction \( u \) s'annule une fois et une seule sur \( \mathbb{R} \).
   d) En déduire l'existence d'une tangente unique à la courbe \( (C) \) passant par le point \( O \).

La courbe \( (C) \) et la courbe \( I \) sont données en annexe, page 6. Tracer cette tangente le plus précisément possible sur cette figure.

4. On considère un réel \( m \) et l'équation \( f(x) = mx \) d'inconnue \( x \). Par lecture graphique et sans justification, donner, suivant les valeurs du réel \( m \), le nombre de solutions de cette équation appartenant à l'intervalle \( ]1; 10] \).

1. Étude de la fonction \( f \) :

La fonction \( f \) est définie par \( f(x) = \ln x - \frac{1}{\ln x} \) sur l'intervalle \( ]1; +\infty[ \).

Dérivée :

\[ f'(x) = \frac{1}{x} + \frac{1}{x (\ln x)^2} = \frac{1}{x}\left(1 + \frac{1}{(\ln x)^2}\right) > 0 \]

La fonction \( f \) est donc strictement croissante sur son domaine, indiquant qu'elle ne peut pas atteindre deux fois la même valeur.

Limites :

• En \( 1^+ \) : \( \ln x \to 0^- \) donc \( f(x) \to -\infty \).
• En \( +\infty \) : \( \ln x \to +\infty \) donc \( f(x) \to +\infty \).

2. a) Asymptote :

\[ \lim_{x \to +\infty} [f(x) - \ln x] = \lim_{x \to +\infty} -\frac{1}{\ln x} = 0 \]

Cette limite indique que la courbe \( \Gamma \) est asymptote horizontale à \( C \) lorsque \( x \) tend vers \( +\infty \).

b) Positions relatives :

Pour déterminer les positions relatives de \( (C) \) et \( \Gamma \), on analyse le signe de \( f(x) - \ln x \) :

• Pour \( x \in ]1; e[ \) : \( \ln x \in ]0; 1[ \) donc \( C \) est située en dessous de \( \Gamma \).
• Pour \( x > e \) : \( \ln x > 1 \) donc \( C \) est au-dessus de \( \Gamma \).

3. Recherche des tangentes passant par \( O \) :

a) Condition de tangence :

L'équation de la tangente \( T_a \) est donnée par : \( y = f'(a)(x - a) + f(a) \).

Pour que cette tangente passe par l'origine \( O \), il faut que \( 0 = -a f'(a) + f(a) \), soit \( f(a) - a f'(a) = 0 \).

b) Équivalence des équations :

Posons \( g(x) = f(x) - x f'(x) \). On peut écrire :

\[ g(x) = \ln x - \frac{1}{\ln x} - x\left(\frac{1}{x} + \frac{1}{x (\ln x)^2}\right) = -\frac{2}{\ln x} - \frac{1}{(\ln x)^2} \]

Cette simplification montre que \( g(x) = 0 \) est équivalent à \( (\ln x)^3 - (\ln x)^2 - \ln x - 1 = 0 \).

c) Étude de \( u(t) = t^3 - t^2 - t - 1 \) :

Calculons la dérivée : \( u'(t) = 3t^2 - 2t - 1 \). Les racines de cette équation sont \( t = 1 \) et \( t = -\frac{1}{3} \).

Analyse des variations :

• Croissante sur \( ]-\infty; -\frac{1}{3}[ \) et \( ]1; +\infty[ \).
• Décroissante sur \( ]-\frac{1}{3}; 1[ \).

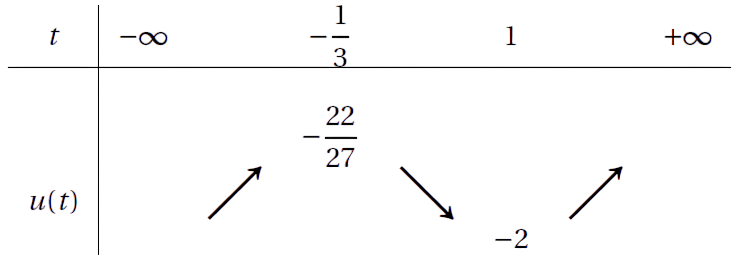
On observe que \( u(1) = -2 \) et \( \lim_{t \to +\infty} u(t) = +\infty \), ce qui garantit l'existence d'un unique \( \alpha \in ]1; +\infty[ \) tel que \( u(\alpha) = 0 \).

d) Conclusion :

Il existe donc une unique tangente \( T_a \) à la courbe \( (C) \) qui passe par l'origine \( O \).

4. Solutions de \( f(x) = mx \) :

Par lecture graphique, on peut conclure :

•     🟢 Pour \( m < f'(a) \) : deux solutions.
•     🟢 Pour \( m = f'(a) \) : une solution (tangente).
•     🟢 Pour \( m > f'(a) \) : aucune solution.