Généralité sur les fonctions. Exploration des notions de convexité, continuité et dérivation...
Les fonctions 📈 constituent le pilier fondamental de l'analyse mathématique. Elles établissent une correspondance unique entre les éléments d'un ensemble de départ (domaine) et ceux d'un ensemble d'arrivée (codomaine). Cette relation permet de modéliser des phénomènes naturels, économiques et technologiques avec une précision remarquable.
La limite d'une fonction f en a, notée \(\lim_{x \to a} f(x) = L\), exprime le comportement de f(x) lorsque x s'approche arbitrairement près de a, sans nécessairement l'atteindre. Cette notion capture l'idée intuitive de "tendance" ou de "rapprochement".
Ces expressions ne permettent pas de conclure directement sur la valeur de la limite. Elles nécessitent une analyse plus poussée pour déterminer le comportement réel de la fonction.
| Forme | Contexte typique |
|---|---|
| \(\frac{\infty}{\infty}\) | Polynômes de même degré |
| \(\frac{0}{0}\) | Fonctions s'annulant simultanément |
| \(\infty - \infty\) | Différence de fonctions divergentes |
| \(0 \times \infty\) | Produit fonction nulle × fonction divergente |
| \(1^{\infty}\) | Fonctions exponentielles |
| \(0^0\) | Fonctions puissance particulières |
| \(\infty^0\) | Fonctions puissance avec exposant nul |
Calculer \(\lim_{x \to 1} \frac{x^2 - 1}{x - 1}\)
Étape 1 : Vérification de la forme indéterminée
Substitution directe : \(\frac{1^2 - 1}{1 - 1} = \frac{0}{0}\) ✓
Étape 2 : Factorisation du numérateur
\(x^2 - 1 = (x - 1)(x + 1)\)
Donc : \(\frac{x^2 - 1}{x - 1} = \frac{(x - 1)(x + 1)}{x - 1} = x + 1\) pour \(x \neq 1\)
Étape 3 : Calcul de la limite
\(\lim_{x \to 1} (x + 1) = 1 + 1 = 2\)
Conclusion : La limite vaut 2
La dérivée de f en a mesure le taux de variation instantané de la fonction en ce point. Elle se définit comme la limite du taux d'accroissement :
Interprétation géométrique : La dérivée f'(a) correspond au coefficient directeur de la tangente à la courbe au point d'abscisse a.
Interprétation physique : Si f(t) représente la position d'un mobile au temps t, alors f'(t) est sa vitesse instantanée.
| Règle | Formule |
|---|---|
| Somme | \((u + v)' = u' + v'\) |
| Produit | \((uv)' = u'v + uv'\) |
| Quotient | \((\frac{u}{v})' = \frac{u'v - uv'}{v^2}\) |
| Composition | \((u \circ v)' = (u' \circ v) \times v'\) |
| Puissance | \((x^n)' = nx^{n-1}\) |
| Exponentielle | \((e^x)' = e^x\) |
Fonction : \(f(x) = (2x^3 + 5x)e^x\)
Méthode : Règle du produit \((uv)' = u'v + uv'\)
Avec \(u = 2x^3 + 5x\) et \(v = e^x\)
\(u' = 6x^2 + 5\) et \(v' = e^x\)
Résultat : \(f'(x) = (6x^2 + 5)e^x + (2x^3 + 5x)e^x\)
\(f'(x) = (2x^3 + 6x^2 + 5x + 5)e^x\)
Une fonction f est continue en a si elle satisfait trois conditions simultanées :
Théorème fondamental : Toute fonction dérivable est continue, mais la réciproque est fausse (contre-exemple : \(f(x) = |x|\) en 0).
Une fonction f est convexe sur un intervalle I si pour tous points A et B de sa courbe, le segment [AB] est situé au-dessus de la courbe.
Caractérisation par la dérivée seconde :
Fonction convexe : "Forme de U" - tournée vers le haut
Fonction concave : "Forme de ∩" - tournée vers le bas
Un point d'inflexion marque une transition dans la concavité de la fonction. Propriétés caractéristiques :
Soit f une fonction continue sur un intervalle fermé \([a, b]\). Pour tout réel k compris entre \(f(a)\) et \(f(b)\), il existe au moins un réel c appartenant à \([a, b]\) tel que \(f(c) = k\).
Conditions d'application :
Utilisations principales :
Exemple d'application :
Montrer que l'équation \(x^3 + x - 1 = 0\) admet une solution dans \([0,1]\) :
1. Soit \(f(x) = x^3 + x - 1\). Cette fonction est continue sur \(\mathbb{R}\) donc sur \([0,1]\)
2. \(f(0) = -1\) et \(f(1) = 1\)
3. Comme \(0 \in [-1,1]\) et \(f(0) < 0 < f(1)\), le TVI garantit l'existence d'au moins un \(c \in [0,1]\) tel que \(f(c) = 0\)
Corollaire de Bolzano :
Si \(f\) est continue sur \([a,b]\) et \(f(a) \cdot f(b) < 0\), alors \(\exists c \in ]a,b[\) tel que \(f(c) = 0\)
Interprétation géométrique :
Une fonction continue ne peut "sauter" par-dessus une valeur horizontale sans la croiser.
Énoncé : Soit \(f\) une fonction continue de \([a,b]\) dans \([a,b]\). Alors \(f\) admet au moins un point fixe, c'est-à-dire qu'il existe \(c \in [a,b]\) tel que \(f(c) = c\).
Démonstration par le TVI :
Considérons la fonction \(g(x) = f(x) - x\) sur \([a,b]\).
Applications :
Fonctions strictement monotones :
Contre-exemples et limitations :
Problème : Trouver les dimensions d'un enclos rectangulaire de périmètre fixé qui maximise l'aire.
Solution :
Résultat : Le carré est la solution optimale.
Ces outils mathématiques permettent de décrire et prédire les comportements des systèmes naturels et artificiels
Calculez la limite suivante :
\[
\lim_{x \to +\infty} \left( \frac{3x^2 + 5}{2x^2 - 7} \right)
\]
Trouvez la limite suivante :
\[
\lim_{x \to 2} (x^3 - 8)
\]
Si \( f(x) = \frac{x^2 - 1}{x - 1} \), calculez la limite suivante :
\[
\lim_{x \to 1} f(x)
\]
Montrez que :
\[
\lim_{x \to +\infty} \left( \frac{5x^3 + 2}{2x^3 + 3x^2} \right) = \frac{5}{2}
\]
en utilisant la comparaison avec des fonctions simples.
Calculez la limite suivante en utilisant la forme indéterminée :
\[
\lim_{x \to 0} \frac{\sin(3x)}{x}
\]
Calculez les limites à droite et à gauche de la fonction suivante au point \(x = 0\) :
\[
f(x) = \begin{cases}
x^2 & \text{si } x < 0 \\
2x & \text{si } x \geq 0
\end{cases}
\]
Calculez la limite suivante :
\[
\lim_{x \to +\infty} \left( e^{-x} + 3 \right)
\]
Trouvez la limite suivante :
\[
\lim_{x \to 0^+} \ln(x)
\]
| \(\frac{0}{0}\) | Fonctions s'annulant simultanément |
| \(\frac{\infty}{\infty}\) | Croissances comparées |
| \(0 \times \infty\) | Produit fonction nulle × divergente |
| \(\infty - \infty\) | Différence de fonctions divergentes |
| \(1^{\infty}\), \(0^0\), \(\infty^0\) | Formes exponentielles indéterminées |
Principe : Factoriser pour simplifier les expressions rationnelles.
\[ \lim_{x \to 2} \frac{x^2 - 4}{x - 2} \]
Résolution :
\[ x^2 - 4 = (x - 2)(x + 2) \]
\[ \frac{(x-2)(x+2)}{x-2} = x+2 \quad (x \neq 2) \]
\[ \lim_{x \to 2} (x+2) = 4 \]
Principe : Éliminer les radicaux en multipliant par l'expression conjuguée.
\[ \lim_{x \to 0} \frac{\sqrt{x+4}-2}{x} \]
Résolution :
Multiplier par le conjugué \(\sqrt{x+4}+2\) :
\[ \frac{(\sqrt{x+4}-2)(\sqrt{x+4}+2)}{x(\sqrt{x+4}+2)} = \frac{x+4-4}{x(\sqrt{x+4}+2)} \]
\[ = \frac{x}{x(\sqrt{x+4}+2)} = \frac{1}{\sqrt{x+4}+2} \]
\[ \lim_{x \to 0} \frac{1}{\sqrt{4}+2} = \frac{1}{4} \]
Si \(\lim_{x\to a} \frac{f(x)}{g(x)}\) est de la forme \(\frac{0}{0}\) ou \(\frac{\infty}{\infty}\) et que \(\lim_{x\to a} \frac{f'(x)}{g'(x)}\) existe, alors :
\[ \lim_{x\to a} \frac{f(x)}{g(x)} = \lim_{x\to a} \frac{f'(x)}{g'(x)} \]
\[ \lim_{x \to 0} \frac{\sin x}{x} \]
Étapes :
Si après une application, on obtient encore une forme indéterminée, on peut réappliquer la règle :
\[ \lim_{x \to 0} \frac{x - \sin x}{x^3} \]
Première application : \(\frac{1 - \cos x}{3x^2}\) (encore \(\frac{0}{0}\))
Deuxième application : \(\frac{\sin x}{6x} = \frac{1}{6}\)
Principe : Substituer pour ramener à une limite connue ou plus simple.
\[ \lim_{x \to 0} \frac{\sin(3x)}{x} \]
Résolution :
Poser \(u = 3x\), alors \(x = \frac{u}{3}\) et \(x \to 0 \Rightarrow u \to 0\) :
\[ \lim_{u \to 0} \frac{\sin u}{\frac{u}{3}} = \lim_{u \to 0} \frac{3\sin u}{u} = 3 \times 1 = 3 \]
Principe : Remplacer les fonctions par leurs développements limités.
Formule de Taylor : Pour une fonction \(f\) de classe \(C^{n+1}\) au voisinage de \(a\) :
\[ \small \begin{align*} f(x) &= f(a) + f'(a)(x-a) + \\ & \quad \frac{f''(a)}{2!}(x-a)^2 + \cdots + \\ & \quad \frac{f^{(n)}(a)}{n!}(x-a)^n + R_n(x) \end{align*} \]où \(R_n(x)\) est le reste.
\[ \lim_{x \to 0} \frac{e^x - 1 - x}{x^2} \]
Résolution :
Développement : \(e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots\)
Donc : \(e^x - 1 - x = \frac{x^2}{2} + \frac{x^3}{6} + \ldots\)
\[ \lim_{x \to 0} \frac{\frac{x^2}{2} + \frac{x^3}{6} + \ldots}{x^2} = \frac{1}{2} \]
Principe : Transformer les formes \(0 \times \infty\) ou \(\infty - \infty\) en formes \(\frac{0}{0}\) ou \(\frac{\infty}{\infty}\).
Forme \(0 \times \infty\) :
\[ \lim_{x \to 0^+} x \ln x = \lim_{x \to 0^+} \frac{\ln x}{\frac{1}{x}} \]
Forme \(\frac{-\infty}{\infty}\), applicable par L'Hôpital.
Forme \(\infty - \infty\) :
\[ \lim_{x \to \infty} (\sqrt{x^2 + x} - x) \]
Multiplier par le conjugué :
\[ \begin{align*} \frac{(\sqrt{x^2 + x} - x)(\sqrt{x^2 + x} + x)}{\sqrt{x^2 + x} + x} &= \\ \frac{x}{x(1 + \sqrt{1 + \frac{1}{x}})} &= \\ \frac{1}{2} \end{align*} \]𝐿𝑎 𝑑𝑒́𝑟𝑖𝑣𝑎𝑡𝑖𝑜𝑛 𝑐𝑜𝑛𝑠𝑖𝑠𝑡𝑒 𝑎̀ 𝑑𝑒́𝑡𝑒𝑟𝑚𝑖𝑛𝑒𝑟 𝑙𝑎 𝑑𝑒́𝑟𝑖𝑣𝑒́𝑒 𝑑'𝑢𝑛𝑒 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(f\), 𝑞𝑢𝑖 𝑟𝑒𝑝𝑟𝑒́𝑠𝑒𝑛𝑡𝑒 𝑙𝑒 𝑡𝑎𝑢𝑥 𝑑𝑒 𝑣𝑎𝑟𝑖𝑎𝑡𝑖𝑜𝑛 𝑑𝑒 \(f\) 𝑝𝑎𝑟 𝑟𝑎𝑝𝑝𝑜𝑟𝑡 𝑎̀ \(x\). 𝑂𝑛 𝑛𝑜𝑡𝑒 𝑙𝑎 𝑑𝑒́𝑟𝑖𝑣𝑒́𝑒 𝑑𝑒 \(f\) 𝑒𝑛 \(x\) 𝑝𝑎𝑟 \(f'(x)\).
• 𝑅𝑒̀𝑔𝑙𝑒 𝑑𝑒 𝑙𝑎 𝑠𝑜𝑚𝑚𝑒 : \((f + g)' = f' + g'\)
• 𝑅𝑒̀𝑔𝑙𝑒 𝑑𝑢 𝑝𝑟𝑜𝑑𝑢𝑖𝑡 : \((f \cdot g)' = f' \cdot g + f \cdot g'\)
• 𝑅𝑒̀𝑔𝑙𝑒 𝑑𝑢 𝑞𝑢𝑜𝑡𝑖𝑒𝑛𝑡 : \(\left(\frac{f}{g}\right)' = \frac{f' \cdot g - f \cdot g'}{g^2}\)
• 𝑃𝑜𝑢𝑟 \(f(x) = x^2\), 𝑜𝑛 𝑎 \(f'(x) = 2x\).
• 𝑃𝑜𝑢𝑟 \(g(x) = \sin(x)\), 𝑜𝑛 𝑎 \(g'(x) = \cos(x)\).
𝑈𝑛𝑒 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(f\) 𝑒𝑠𝑡 𝑑𝑖𝑡𝑒 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑠𝑢𝑟 𝑢𝑛 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 𝑠𝑖, 𝑝𝑜𝑢𝑟 𝑡𝑜𝑢𝑠 \(x_1, x_2\) 𝑑𝑎𝑛𝑠 𝑐𝑒𝑡 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 𝑒𝑡 𝑝𝑜𝑢𝑟 𝑡𝑜𝑢𝑡 \(\lambda \in [0, 1]\) :\[f(\lambda x_1 + (1 - \lambda) x_2) \leq \lambda f(x_1) + (1 - \lambda) f(x_2)\]
• 𝐺𝑟𝑎𝑝ℎ𝑖𝑞𝑢𝑒𝑚𝑒𝑛𝑡, 𝑙𝑎 𝑐𝑜𝑢𝑟𝑏𝑒 𝑑𝑒 \(f\) 𝑒𝑠𝑡 𝑠𝑖𝑡𝑢𝑒́𝑒 𝑎𝑢-𝑑𝑒𝑠𝑠𝑢𝑠 𝑑𝑒 𝑙𝑎 𝑙𝑖𝑔𝑛𝑒 𝑗𝑜𝑖𝑔𝑛𝑎𝑛𝑡 𝑙𝑒𝑠 𝑝𝑜𝑖𝑛𝑡𝑠 \((x_1, f(x_1))\) 𝑒𝑡 \((x_2, f(x_2))\).
• 𝑈𝑛𝑒 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 𝑒𝑠𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑠𝑖 𝑠𝑎 𝑑𝑒́𝑟𝑖𝑣𝑒́𝑒 𝑐𝑟𝑜𝑖̂𝑡.
• 𝐿𝑎 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(f(x) = x^2\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑠𝑢𝑟 \(\mathbb{R}\).
• 𝐿𝑎 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(g(x) = e^x\) 𝑒𝑠𝑡 𝑒́𝑔𝑎𝑙𝑒𝑚𝑒𝑛𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒.
𝑈𝑛𝑒 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(f\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑠𝑢𝑟 𝑢𝑛 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 𝑠𝑖 𝑠𝑎 𝑑𝑒́𝑟𝑖𝑣𝑒́𝑒 \(f'\) 𝑒𝑠𝑡 𝑐𝑟𝑜𝑖𝑠𝑠𝑎𝑛𝑡𝑒 𝑠𝑢𝑟 𝑐𝑒𝑡 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒.
• 𝑆𝑖 \(f''(x) \geq 0\) 𝑝𝑜𝑢𝑟 𝑡𝑜𝑢𝑡 \(x\) 𝑑𝑎𝑛𝑠 𝑢𝑛 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒, 𝑎𝑙𝑜𝑟𝑠 \(f\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑠𝑢𝑟 𝑐𝑒𝑡 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒.
• 𝑆𝑖 \(f\) 𝑒𝑠𝑡 𝑑𝑒𝑢𝑥 𝑓𝑜𝑖𝑠 𝑑𝑒́𝑟𝑖𝑣𝑎𝑏𝑙𝑒 𝑒𝑡 \(f''(x) > 0\), 𝑎𝑙𝑜𝑟𝑠 \(f\) 𝑒𝑠𝑡 𝑠𝑡𝑟𝑖𝑐𝑡𝑒𝑚𝑒𝑛𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒.
• 𝑃𝑜𝑢𝑟 \(f(x) = x^3\), 𝑜𝑛 𝑎 \(f''(x) = 6x\). 𝐿𝑎 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 𝑒𝑠𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑝𝑜𝑢𝑟 \(x \geq 0\).
• 𝑃𝑜𝑢𝑟 \(g(x) = x^4\), 𝑜𝑛 𝑎 \(g''(x) = 12x^2\), donc \(g\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑣𝑒𝑥𝑒 𝑠𝑢𝑟 𝑡𝑜𝑢𝑡 \(\mathbb{R}\).
𝑈𝑛𝑒 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(f\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒 𝑒𝑛 𝑢𝑛 𝑝𝑜𝑖𝑛𝑡 \(a\) 𝑠𝑖 : \[lim_{x \to a} f(x) = f(a)\]
• 𝐿𝑒𝑠 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛𝑠 𝑝𝑜𝑙𝑦𝑛𝑜𝑚𝑖𝑎𝑙𝑒𝑠 𝑒𝑡 𝑒𝑥𝑝𝑜𝑛𝑒𝑛𝑡𝑖𝑒𝑙𝑙𝑒𝑠 𝑠𝑜𝑛𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒𝑠 𝑠𝑢𝑟 \(\mathbb{R}\).
• 𝑆𝑖 \(f\) et \(g\) 𝑠𝑜𝑛𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒𝑠, 𝑎𝑙𝑜𝑟𝑠 \(f + g\), \(f \cdot g\) 𝑒𝑡 \(\frac{f}{g}\) (si \(g \neq 0\)) 𝑠𝑜𝑛𝑡 𝑎𝑢𝑠𝑠𝑖 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒𝑠.
• 𝐿𝑎 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(f(x) = \sin(x)\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒 𝑠𝑢𝑟 \(\mathbb{R}\).
• 𝐿𝑎 𝑓𝑜𝑛𝑐𝑡𝑖𝑜𝑛 \(g(x) = \frac{1}{x}\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒 𝑠𝑢𝑟 \(\mathbb{R} \setminus \{0\}\).
𝐿𝑒 𝑡ℎ𝑒́𝑜𝑟𝑒̀𝑚𝑒 𝑑𝑒𝑠 𝑣𝑎𝑙𝑒𝑢𝑟𝑠 𝑖𝑛𝑡𝑒𝑟𝑚𝑒́𝑑𝑖𝑎𝑖𝑟𝑒𝑠 𝑠𝑡𝑖𝑝𝑢𝑙𝑒 𝑞𝑢𝑒 𝑠𝑖 \(f\) 𝑒𝑠𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒 𝑠𝑢𝑟 𝑢𝑛 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 \([a, b]\) 𝑒𝑡 \(N\) 𝑒𝑠𝑡 𝑢𝑛 𝑛𝑜𝑚𝑏𝑟𝑒 𝑒𝑛𝑡𝑟𝑒 \(f(a)\) 𝑒𝑡 \(f(b)\), 𝑎𝑙𝑜𝑟𝑠 𝑖𝑙 𝑒𝑥𝑖𝑠𝑡𝑒 𝑎𝑢 𝑚𝑜𝑖𝑛𝑠 𝑢𝑛 \(c \in [a, b]\) 𝑡𝑒𝑙 𝑞𝑢𝑒 \(f(c) = N\).
• 𝐶𝑒 𝑡ℎ𝑒́𝑜𝑟𝑒̀𝑚𝑒 𝑒𝑠𝑡 𝑓𝑜𝑛𝑑𝑎𝑚𝑒𝑛𝑡𝑎𝑙 𝑝𝑜𝑢𝑟 𝑑𝑒́𝑚𝑜𝑛𝑡𝑟𝑒𝑟 𝑙'𝑒𝑥𝑖𝑠𝑡𝑒𝑛𝑐𝑒 𝑑𝑒 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛𝑠 𝑑'𝑒́𝑞𝑢𝑎𝑡𝑖𝑜𝑛𝑠 𝑑𝑎𝑛𝑠 𝑢𝑛 𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 𝑑𝑜𝑛𝑛𝑒́.
• 𝐼𝑙 𝑛𝑒 𝑛𝑒́𝑐𝑒𝑠𝑠𝑖𝑡𝑒 𝑝𝑎𝑠 𝑞𝑢𝑒 \(f\) 𝑠𝑜𝑖𝑡 𝑑𝑒́𝑟𝑖𝑣𝑎𝑏𝑙𝑒, 𝑠𝑒𝑢𝑙𝑒𝑚𝑒𝑛𝑡 𝑐𝑜𝑛𝑡𝑖𝑛𝑢𝑒.
𝑃𝑜𝑢𝑟 \(f(x) = x^3 - x\) 𝑠𝑢𝑟 𝑙'𝑖𝑛𝑡𝑒𝑟𝑣𝑎𝑙𝑙𝑒 \([-2, 2]\), \(f(-2) = -6\) et \(f(2) = 6\). 𝑃𝑎𝑟 𝑙𝑒 𝑡ℎ𝑒́𝑜𝑟𝑒̀𝑚𝑒, 𝑖𝑙 𝑒𝑥𝑖𝑠𝑡𝑒 𝑢𝑛 \(c\) 𝑡𝑒𝑙 𝑞𝑢𝑒 \(f(c) = 0\).
Trouvez la dérivée de la fonction suivante :
\[
f(x) = 4x^3 - 2x^2 + 7x - 5
\]
Calculez la dérivée de la fonction suivante :
\[
g(x) = \sin(2x^2 + 3)
\]
Montrez que la fonction suivante est continue en \(x = 1\) :
\[
h(x) = \begin{cases}
2x + 1 & \text{si } x < 1 \\
3 & \text{si } x = 1 \\
x^2 & \text{si } x > 1
\end{cases}
\]
Déterminez si la fonction suivante est convexe sur \(\mathbb{R}\) :
\[
f(x) = x^4 - 4x^2 + 3
\]
Justifiez votre réponse en examinant la dérivée seconde.
Étudiez la monotonicité de la fonction suivante :
\[
f(x) = x^3 - 3x^2 + 2
\]
Trouvez les intervalles où \(f\) est croissante ou décroissante.
Appliquez le théorème des valeurs intermédiaires à la fonction suivante sur l'intervalle \([-1, 2]\) :
\[
f(x) = x^2 - 2
\]
Montrez qu'il existe un \(c\) tel que \(f(c) = 0\).
Trouvez la dérivée de la fonction \(f(x) = \ln(x^2 + 1)\) et évaluez-la en \(x = 1\).
Montrez que la fonction \(g(x) = x^2 + 2x + 1\) est convexe sur \(\mathbb{R}\) en utilisant la dérivée.
Les fonctions trigonométriques sont définies à partir du cercle trigonométrique de rayon 1 centré à l'origine.
| θ | cos(θ) | sin(θ) | tan(θ) |
|---|---|---|---|
| 0 | 1 | 0 | 0 |
| \(\frac{\pi}{6}\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{3}\) |
| \(\frac{\pi}{4}\) | \(\frac{\sqrt{2}}{2}\) | \(\frac{\sqrt{2}}{2}\) | 1 |
| \(\frac{\pi}{3}\) | \(\frac{1}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\sqrt{3}\) |
| \(\frac{\pi}{2}\) | 0 | 1 | ∞ |
| x | 0 | \(\frac{\pi}{2}\) | \(\pi\) | \(\frac{3\pi}{2}\) | \(2\pi\) |
|---|---|---|---|---|---|
| cos(x) | 1 | 0 | -1 | 0 | 1 |
| Variation | ↘ | ↘ | ↗ | ↗ | - |
| x | 0 | \(\frac{\pi}{2}\) | \(\pi\) | \(\frac{3\pi}{2}\) | \(2\pi\) |
|---|---|---|---|---|---|
| sin(x) | 0 | 1 | 0 | -1 | 0 |
| Variation | ↗ | ↘ | ↘ | ↗ | - |
Simplifier : \(\cos(3x)\) en fonction de \(\cos(x)\)
\(\cos(3x) = \cos(2x + x)\)
\(= \cos(2x)\cos(x) - \sin(2x)\sin(x)\)
\(= (2\cos^2(x) - 1)\cos(x) - 2\sin(x)\cos(x)\sin(x)\)
\(= 2\cos^3(x) - \cos(x) - 2\sin^2(x)\cos(x)\)
\(= 2\cos^3(x) - \cos(x) - 2(1-\cos^2(x))\cos(x)\)
Résultat : \(\cos(3x) = 4\cos^3(x) - 3\cos(x)\)
Cette limite est la plus importante et permet de dériver toutes les autres.
Pour \(0 < x < \frac{\pi}{2}\), on encadre \(\sin(x)\) dans le cercle trigonométrique :
Inégalité clé : \(\sin(x) < x < \tan(x)\)
En divisant par \(\sin(x) > 0\) :
\(1 < \frac{x}{\sin(x)} < \frac{1}{\cos(x)}\)
Donc : \(\cos(x) < \frac{\sin(x)}{x} < 1\)
Quand \(x \to 0^+\), \(\cos(x) \to 1\), donc par encadrement :
\(\lim_{x \to 0^+} \frac{\sin(x)}{x} = 1\)
Calculer : \(\lim_{x \to 0} \frac{\sin(3x)}{2x}\)
\(\frac{\sin(3x)}{2x} = \frac{3}{2} \cdot \frac{\sin(3x)}{3x}\)
Posons \(u = 3x\), alors \(u \to 0\) quand \(x \to 0\)
\(\lim_{x \to 0} \frac{\sin(3x)}{2x} = \frac{3}{2} \lim_{u \to 0} \frac{\sin(u)}{u} = \frac{3}{2} \times 1 = \frac{3}{2}\)
| Équation | Solutions |
|---|---|
| \(\cos(x) = a\) | \(x = \pm \arccos(a) + 2k\pi\) |
| \(\sin(x) = a\) | \(x = \arcsin(a) + 2k\pi\) ou \(x = \pi - \arcsin(a) + 2k\pi\) |
| \(\tan(x) = a\) | \(x = \arctan(a) + k\pi\) |
| \(\cos(x) = \cos(\alpha)\) | \(x = \pm \alpha + 2k\pi\) |
| \(\sin(x) = \sin(\alpha)\) | \(x = \alpha + 2k\pi\) ou \(x = \pi - \alpha + 2k\pi\) |
| \(\tan(x) = \tan(\alpha)\) | \(x = \alpha + k\pi\) |
| Inéquation | Méthode de résolution |
|---|---|
| \(\cos(x) \geq a\) | Utiliser le cercle trigonométrique |
| \(\sin(x) \leq a\) | Déterminer les arcs correspondants |
| \(\tan(x) > a\) | Considérer la périodicité \(\pi\) |
| \(f(x) \geq g(x)\) | Étudier \(f(x) - g(x) \geq 0\) |
Résoudre : \(2\cos^2(x) - 3\cos(x) + 1 = 0\)
Étape 1 : Changement de variable
Posons \(u = \cos(x)\), alors : \(2u^2 - 3u + 1 = 0\)
Discriminant : \(\Delta = 9 - 8 = 1\)
Solutions : \(u_1 = \frac{3+1}{4} = 1\) et \(u_2 = \frac{3-1}{4} = \frac{1}{2}\)
Étape 2 : Retour à la variable x
\(\cos(x) = 1 \Rightarrow x = 2k\pi\)
\(\cos(x) = \frac{1}{2} \Rightarrow x = \pm \frac{\pi}{3} + 2k\pi\)
Solutions : \(x \in \{2k\pi, \pm \frac{\pi}{3} + 2k\pi\}\)
Résoudre : \(\sin(2x) = \sin(x)\)
Étape 1 : Développement
\(2\sin(x)\cos(x) = \sin(x)\)
\(2\sin(x)\cos(x) - \sin(x) = 0\)
\(\sin(x)(2\cos(x) - 1) = 0\)
Étape 2 : Résolution
\(\sin(x) = 0 \Rightarrow x = k\pi\)
\(2\cos(x) - 1 = 0 \Rightarrow \cos(x) = \frac{1}{2} \Rightarrow x = \pm \frac{\pi}{3} + 2k\pi\)
Solutions : \(x \in \{k\pi, \pm \frac{\pi}{3} + 2k\pi\}\)
Résoudre : \(\cos(x) \geq \frac{1}{2}\) sur \([0, 2\pi]\)
Étape 1 : Résolution de l'équation associée
\(\cos(x) = \frac{1}{2}\) pour \(x = \frac{\pi}{3}\) et \(x = \frac{5\pi}{3}\)
Étape 2 : Utilisation du cercle trigonométrique
Le cosinus est \(\geq \frac{1}{2}\) entre \(0\) et \(\frac{\pi}{3}\), puis entre \(\frac{5\pi}{3}\) et \(2\pi\)
Solution : \(x \in \left[0, \frac{\pi}{3}\right] \cup \left[\frac{5\pi}{3}, 2\pi\right]\)
Résoudre : \(2\cos^2(x) - 3\cos(x) + 1 \leq 0\) sur \([0, 2\pi]\)
Étape 1 : Changement de variable
Posons \(u = \cos(x)\), alors : \(2u^2 - 3u + 1 \leq 0\)
Factorisation : \((2u - 1)(u - 1) \leq 0\)
Solutions : \(\frac{1}{2} \leq u \leq 1\)
Étape 2 : Retour à la variable x
\(\frac{1}{2} \leq \cos(x) \leq 1\)
Sur \([0, 2\pi]\) : \(\cos(x) = \frac{1}{2}\) pour \(x = \frac{\pi}{3}\) et \(x = \frac{5\pi}{3}\)
Solution : \(x \in \left[0, \frac{\pi}{3}\right] \cup \left[\frac{5\pi}{3}, 2\pi\right]\)
Résoudre : \(\sin(x) > \frac{\sqrt{3}}{2}\) sur \([0, 2\pi]\)
Étape 1 : Résolution de l'équation associée
\(\sin(x) = \frac{\sqrt{3}}{2}\) pour \(x = \frac{\pi}{3}\) et \(x = \frac{2\pi}{3}\)
Étape 2 : Analyse sur le cercle trigonométrique
Le sinus est \(> \frac{\sqrt{3}}{2}\) entre \(\frac{\pi}{3}\) et \(\frac{2\pi}{3}\)
Solution : \(x \in \left(\frac{\pi}{3}, \frac{2\pi}{3}\right)\)
Les fonctions trigonométriques trouvent leurs origines dans l'astronomie antique. Hipparque (IIe siècle av. J.-C.) établit les premières tables trigonométriques pour calculer les positions des astres. Le mot "sinus" vient du latin "sinus" (courbe, pli) qui est une traduction erronée de l'arabe "jayb" (poche), lui-même traduction du sanskrit "jīvā" (corde d'arc).
Calculez les valeurs suivantes :
• \(\sin\left(\frac{\pi}{4}\right)\)
• \(\cos\left(\frac{\pi}{3}\right)\)
• \(\tan\left(-\frac{\pi}{6}\right)\)
Déterminez la période des fonctions suivantes :
• \(f(x) = 3\sin(2x)\)
• \(g(x) = -\cos(4x + \frac{\pi}{2})\)
Étudiez les variations de la fonction \(f(x) = \sin(x)\) sur l'intervalle \([-2\pi, 2\pi]\). Indiquez les points critiques, les maximums et les minimums.

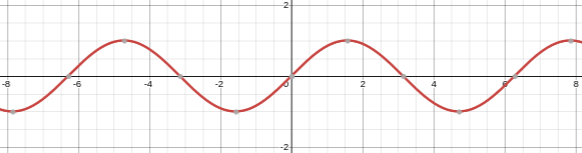
Résolvez l'équation suivante sur l'intervalle \([-π; π]\) :
\[
\cos(x) = \frac{1}{2}
\]
Résolvez l'inéquation suivante sur l'intervalle \([-π; π]\) :
\[
\sin(x) < 0
\]
Résolvez l'équation suivante sur l'intervalle \([-π; π]\) :
\[
\sin(x) = -\frac{\sqrt{3}}{2}
\]
Vérifiez l'identité suivante :
\[
\sin^2(x) + \cos^2(x) = 1
\]
pour \(x = \frac{\pi}{3}\).
Un pont est soutenu par un câble formant un angle de \(30^\circ\) avec le sol. Si la longueur du câble est de 10 mètres, quelle est la hauteur maximale du pont par rapport au sol ? Utilisez la fonction sinus.
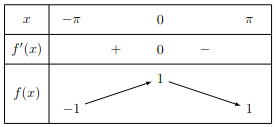
Réaliser une étude complète de la fonction \(cos(x)\) sur l'intervalle \([−\pi,\pi]\).
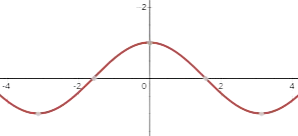
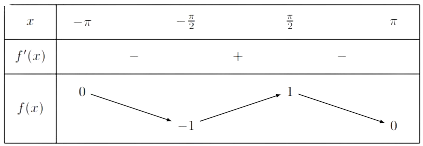
Réaliser une étude complète de la fonction \(sin(x)\) sur l'intervalle \([−\pi,\pi]\).
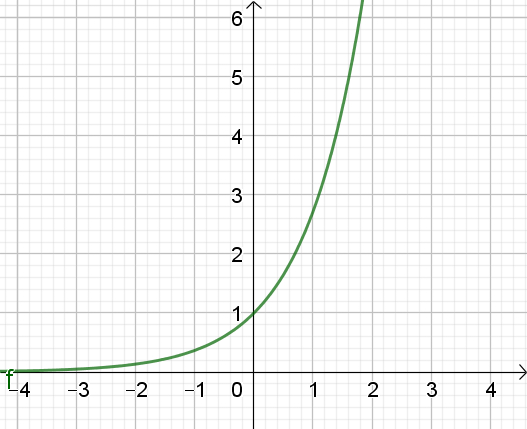
La fonction exponentielle est définie comme l'unique fonction \(f\) telle que \(f'(x) = f(x)\) et \(f(0) = 1\).
| \(e^{a+b} = e^a \times e^b\) | Loi des exposants |
| \(e^{a-b} = \frac{e^a}{e^b}\) | Division d'exponentielles |
| \((e^a)^b = e^{ab}\) | Puissance d'exponentielle |
| \(e^0 = 1\) | Valeur particulière |
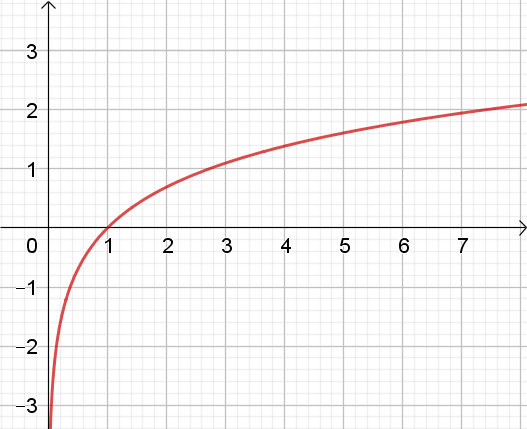
Le logarithme népérien est la fonction réciproque de la fonction exponentielle.
| \(\ln(ab) = \ln a + \ln b\) | Logarithme d'un produit |
| \(\ln\left(\frac{a}{b}\right) = \ln a - \ln b\) | Logarithme d'un quotient |
| \(\ln(a^b) = b \ln a\) | Logarithme d'une puissance |
| \(\ln(1) = 0\) | Valeur particulière |
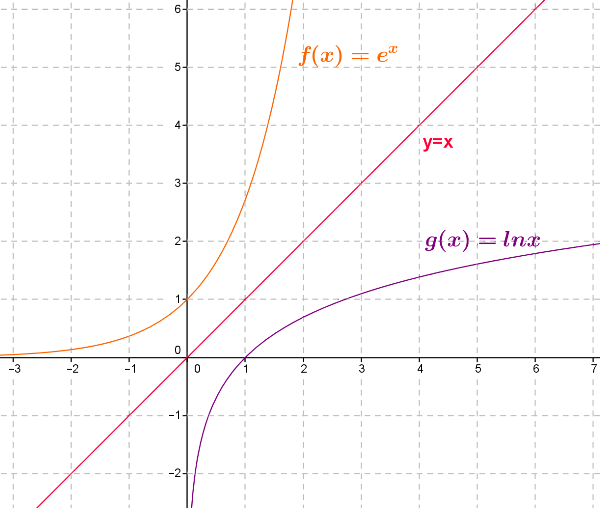
Les fonctions exponentielles et logarithme népérien sont des fonctions réciproques.
Ces limites sont fondamentales pour l'étude des fonctions exponentielles et logarithmiques.
| \(\lim_{x \to +\infty} e^x = +\infty\) | Croissance exponentielle |
| \(\lim_{x \to -\infty} e^x = 0\) | Asymptote horizontale y = 0 |
| \(\lim_{x \to 0} \frac{e^x - 1}{x} = 1\) | Limite remarquable |
| \(\lim_{x \to 0} \frac{e^x - 1 - x}{x^2} = \frac{1}{2}\) | Développement limité d'ordre 2 |
| \(\lim_{x \to +\infty} \frac{e^x}{x} = +\infty\) | Croissance comparée |
| \(\lim_{x \to +\infty} \ln(x) = +\infty\) | Croissance logarithmique |
| \(\lim_{x \to 0^+} \ln(x) = -\infty\) | Asymptote verticale x = 0 |
| \(\lim_{x \to 0} \frac{\ln(1+x)}{x} = 1\) | Limite remarquable |
| \(\lim_{x \to 0} \frac{\ln(1+x) - x}{x^2} = -\frac{1}{2}\) | Développement limité d'ordre 2 |
| \(\lim_{x \to +\infty} \frac{\ln(x)}{x} = 0\) | Croissance comparée |
| \(\lim_{x \to 1} \frac{\ln(x)}{x-1} = 1\) | Dérivée de ln en x = 1 |
| \(\lim_{x \to 0^+} x \ln(x) = 0\) | Forme 0 × (-∞) |
| \(\lim_{x \to 0^+} x^a \ln(x) = 0\) | Pour tout a > 0 |
| \(\lim_{x \to +\infty} x^n e^{-x} = 0\) | Pour tout n > 0 |
| \(\lim_{x \to -\infty} x^n e^x = 0\) | Pour tout n ≥ 0 |
| \(\lim_{x \to 0^+} x^a (\ln(x))^b = 0\) | Pour tout a > 0, b réel |
| \(\lim_{x \to +\infty} (\ln(x))^a x^{-b} = 0\) | Pour tout a réel, b > 0 |
| \(\lim_{x \to +\infty} \frac{\ln(x)}{x^n} = 0\) | Pour tout n > 0 |
| \(\lim_{x \to +\infty} \frac{x^n}{e^x} = 0\) | Pour tout n > 0 |
| \(\lim_{x \to +\infty} \frac{e^x}{x^n} = +\infty\) | Pour tout n > 0 |
| \(\lim_{x \to +\infty} \frac{x^n}{\ln(x)} = +\infty\) | Pour tout n > 0 |
| \(\lim_{x \to +\infty} \frac{(\ln(x))^n}{x^p} = 0\) | Pour tout n > 0, p > 0 |
| \(\lim_{x \to 0^+} \frac{x^n}{|\ln(x)|^p} = 0\) | Pour tout n > 0, p > 0 |
| \(\lim_{x \to 0^+} \frac{|\ln(x)|^n}{x^{-p}} = 0\) | Pour tout n > 0, p > 0 |
| \(\lim_{x \to 0} (1+x)^{\frac{1}{x}} = e\) | Forme 1^∞ |
| \(\lim_{x \to +\infty} \left(1+\frac{1}{x}\right)^x = e\) | Définition de e |
| \(\lim_{x \to 0} \frac{a^x - 1}{x} = \ln(a)\) | Pour a > 0, a ≠ 1 |
| \(\lim_{x \to 0} \frac{\log_a(1+x)}{x} = \frac{1}{\ln(a)}\) | Pour a > 0, a ≠ 1 |
Ces résultats montrent la vitesse de croissance relative des fonctions :
\((\ln(x))^n \ll x^p \ll e^x\) quand \(x \to +\infty\)
(pour tous n, p > 0)
L'exponentielle croît plus vite que toute puissance polynomiale, qui elle-même croît plus vite que toute puissance du logarithme.
Résoudre : \(e^{2x-1} = 3\)
Solution :
En appliquant le logarithme népérien aux deux membres :
\(\ln(e^{2x-1}) = \ln(3)\)
\(2x - 1 = \ln(3)\)
\(x = \frac{1 + \ln(3)}{2}\)
Résoudre : \(\ln(x+2) - \ln(x-1) = \ln(2)\)
Solution :
En utilisant les propriétés du logarithme :
\(\ln\left(\frac{x+2}{x-1}\right) = \ln(2)\)
\(\frac{x+2}{x-1} = 2\)
\(x + 2 = 2(x-1)\)
\(x = 4\)
Calculez les valeurs suivantes :
• \(\ln(e^2)\)
• \(\ln(1)\)
• \(\ln(0.01)\)
Utilisez les propriétés des logarithmes pour simplifier les expressions suivantes :
• \(\ln(3) + \ln(5)\)
• \(\ln\left(\frac{8}{2}\right)\)
• \(2 \ln(4) - \ln(16)\)
Résolvez les équations suivantes :
• \(\ln(x) = 3\)
• \(\ln(x - 1) + \ln(2) = 0\)
Résolvez l'inéquation suivante : \(\ln(x) > 1\)
Calculez les limites suivantes :
• \(\lim_{x \to 0^+} \ln(x)\)
• \(\lim_{x \to +\infty} \ln(x)\)
Étudiez les variations de la fonction \(f(x) = \ln(x)\) sur l'intervalle \((0, +\infty)\) :
• Indiquez si la fonction est croissante ou décroissante.
• Déterminez les points critiques.
Un investissement de 1000 € croît à un taux d'intérêt de 5 % par an, composé annuellement. Utilisez la fonction logarithme pour déterminer combien de temps il faudra pour que l'investissement atteigne 2000 €.
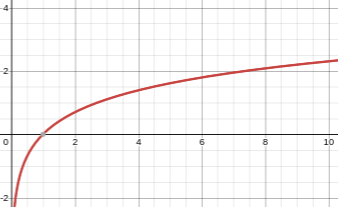
Tracez le graphe de la fonction \(y = \ln(x)\) sur l'intervalle \((0, 10)\). Identifiez les asymptotes et les points d'intersection avec les axes.
Présentez le concept de limite et son importance en analyse. Calculez et expliquez la limite suivante :
\[
\lim_{x \to 1} \frac{x^2 - 1}{x - 1}
\]
Discussion : Parlez de la méthode de simplification, des formes indéterminées et de la continuité.
Étudiez la fonction \(f(x) = x^3 - 3x^2 + 4\).
1. Présentez les étapes pour calculer la dérivée \(f'(x)\).
2. Discutez des points critiques et de leur interprétation graphique.
3. Examinez la convexité par \(f''(x)\).
Discussion : Parlez de l'importance de la dérivation pour comprendre le comportement des fonctions et de la relation entre dérivées et courbes.
Résolvez et présentez l'équation suivante sur l'intervalle \([-π; π]\) :
\[
\sin(x) + \sin(2x) = 0
\]
Discussion : Discutez des identités trigonométriques utilisées pour simplifier l'équation et des méthodes graphiques pour visualiser les solutions.
Présentez la fonction logarithme népérien et sa relation avec l'exponentielle. Résolvez l'équation :
\[
\ln(2x + 1) - \ln(x) = 1
\]
Discussion : Expliquez l'utilisation des propriétés des logarithmes et la signification des solutions dans un contexte pratique.
Modélisez une situation économique où la demande \(D\) d'un produit est donnée par \(D(p) = 100 - 5p\) et le coût de production par \(C(p) = 20 + 2p\).
1. Établissez la fonction de profit \(P(p) = D(p) - C(p)\).
2. Présentez les étapes pour maximiser le profit.
Discussion : Parlez de l'importance des mathématiques dans la prise de décision économique et des outils utilisés pour analyser les données.

Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !