Exploration de la géométrie dans l'espace
Vous êtes ingénieur·e navigation à l'Agence Spatiale Européenne. La sonde Euclidia, lancée vers Jupiter dans le cadre d'une mission d'exploration des lunes galiléennes, a perdu le contact avec le centre de contrôle terrestre. Son dernier signal télémétrique, reçu il y a 3 heures, indiquait une trajectoire rectiligne définie par le point A(1,2,-1) et le vecteur directeur u(3,-1,2). Votre mission : localiser la sonde et programmer un drone de récupération pour rétablir le contact.
1.1 Déterminez l'équation paramétrique de la trajectoire (droite Δ) de la sonde Euclidia.
1.2 Un satellite relais stratégique se trouve dans le plan Π d'équation \( 2x - y + 3z = 5 \). Pour établir une communication de secours, vérifiez que la trajectoire Δ n'est pas parallèle au plan Π en comparant le vecteur directeur de Δ avec le vecteur normal au plan.
1.3 Calculez les coordonnées exactes du point d'intersection I entre la trajectoire Δ et le plan Π du satellite relais. Ce point représente la position où la sonde pourrait établir une communication de secours.
2.1 Les ingénieurs ont identifié que les vecteurs v(1,5,1) et w(-1,1,1) correspondent aux axes principaux du système de communication du satellite relais. Vérifiez que ces vecteurs forment effectivement une base du plan Π.
2.2 Pour calibrer le système de communication, décomposez le vecteur AI (vecteur déplacement de la sonde) dans cette base de communication.
Pour récupérer la sonde, vous devez programmer un drone autonome avec une trajectoire rectiligne optimisée. Le drone doit minimiser la consommation d'énergie tout en garantissant l'interception.
3.1 Le drone part de la station spatiale B(0,3,-2) et doit intercepter la trajectoire Δ. Déterminez le vecteur directeur d de sa trajectoire sachant qu'il doit être orthogonal au vecteur u pour une approche optimale (économie d'énergie).
3.2 Calculez la distance minimale entre la station B et la trajectoire Δ. Démontrez que cette distance est égale à \( \frac{\sqrt{165}}{7} \) unités spatiales.
Figure : Représentation 3D de la mission spatiale - Trajectoire de la sonde Euclidia, plan du satellite relais et optimisation du drone de récupération
Défi avancé : La sonde Euclidia se déplace à une vitesse constante de \( \sqrt{14} \) unités/seconde le long de sa trajectoire, tandis que le drone de récupération peut atteindre une vitesse maximale de \( \sqrt{7} \) unités/seconde. Déterminez le point optimal d'interception en tenant compte de ces contraintes de vitesse et du temps écoulé depuis la perte de contact.
La géométrie dans l'espace constitue une extension naturelle des concepts bidimensionnels vers un univers tridimensionnel. Cette discipline mathématique trouve ses applications dans de nombreux domaines : de la physique théorique à l'ingénierie structurale, en passant par l'infographie 3D et la robotique moderne.
Contrairement à la géométrie plane qui se limite aux notions de longueur et d'angle, la géométrie spatiale introduit des concepts fondamentaux comme les volumes, les orientations dans l'espace et les relations complexes entre objets tridimensionnels. Elle permet de modéliser des phénomènes physiques réels et de résoudre des problèmes concrets d'optimisation spatiale.
Figure 1 : Repère orthonormé direct dans l'espace tridimensionnel
Le produit scalaire de deux vecteurs \(\vec{u}\) et \(\vec{v}\) dans l'espace est défini comme le nombre réel :
où \(\theta\) est l'angle formé par les deux vecteurs. Cette formule exprime intuitivement la "projection" d'un vecteur sur l'autre.
Si \(\vec{u}\begin{pmatrix}x_1\\y_1\\z_1\end{pmatrix}\) et \(\vec{v}\begin{pmatrix}x_2\\y_2\\z_2\end{pmatrix}\), alors :
Figure 2 : Interprétation géométrique du produit scalaire
Le produit vectoriel de deux vecteurs \(\vec{u}\) et \(\vec{v}\) est un vecteur \(\vec{w}\) tel que :
où \(\vec{n}\) est le vecteur unitaire orthogonal à \(\vec{u}\) et \(\vec{v}\), orienté selon la règle de la main droite.
Si \(\vec{u}\begin{pmatrix}x_1\\y_1\\z_1\end{pmatrix}\) et \(\vec{v}\begin{pmatrix}x_2\\y_2\\z_2\end{pmatrix}\), alors :
Figure 3 : Produit vectoriel et orientation spatiale
Une droite dans l'espace peut être définie de plusieurs façons équivalentes :
Représentation paramétrique :
Point \(A(x_0,y_0,z_0)\) et vecteur directeur \(\vec{u}\begin{pmatrix}a\\b\\c\end{pmatrix}\)
Représentation cartésienne :
Intersection de deux plans non parallèles :
Note : Le vecteur directeur est orthogonal aux vecteurs normaux des deux plans : \(\vec{u} = \vec{n_1} \wedge \vec{n_2}\)
Un plan dans l'espace peut être caractérisé par différentes représentations :
Équation cartésienne :
Point \(A(x_0,y_0,z_0)\) et vecteur normal \(\vec{n}\begin{pmatrix}a\\b\\c\end{pmatrix}\)
Représentation paramétrique :
Point \(A\) et deux vecteurs directeurs \(\vec{u}\), \(\vec{v}\) non colinéaires :
Relation importante : Le vecteur normal est donné par \(\vec{n} = \vec{u} \wedge \vec{v}\)
Figure 4 : Représentation d'un plan et d'une droite dans l'espace
Distance du point \(M(x_1,y_1,z_1)\) au plan \(ax + by + cz + d = 0\) :
Distance du point \(M\) à la droite passant par \(A\) de vecteur directeur \(\vec{u}\) :
Droite et plan :
Deux droites :
Deux plans :
Intersection droite-plan :
Intersection de deux plans :
Test de coplanarité :
Calculer l'angle entre les vecteurs \(\vec{u}\begin{pmatrix}1\\2\\-1\end{pmatrix}\) et \(\vec{v}\begin{pmatrix}3\\0\\1\end{pmatrix}\).
Solution :
\(\vec{u} \cdot \vec{v} = 1 \times 3 + 2 \times 0 + (-1) \times 1 = 2\)
\(\|\vec{u}\| = \sqrt{1^2 + 2^2 + (-1)^2} = \sqrt{6}\)
\(\|\vec{v}\| = \sqrt{3^2 + 0^2 + 1^2} = \sqrt{10}\)
\(\cos(\theta) = \frac{2}{\sqrt{6} \times \sqrt{10}} = \frac{2}{\sqrt{60}} = \frac{1}{\sqrt{15}}\)
Déterminer l'équation du plan passant par \(A(1,2,3)\), \(B(2,1,4)\) et \(C(0,3,2)\).
Solution :
\(\overrightarrow{AB}\begin{pmatrix}1\\-1\\1\end{pmatrix}\), \(\overrightarrow{AC}\begin{pmatrix}-1\\1\\-1\end{pmatrix}\)
\(\vec{n} = \overrightarrow{AB} \wedge \overrightarrow{AC} = \begin{pmatrix}0\\0\\0\end{pmatrix}\)
Les points sont alignés ! Pas de plan unique.
🎯 Problèmes d'angles :
📐 Problèmes géométriques :
📊 Problèmes de distance :
| Opération | Formule |
|---|---|
| Produit scalaire | \(\vec{u} \cdot \vec{v} = x_1x_2 + y_1y_2 + z_1z_2\) |
| Produit vectoriel | \(\vec{u} \wedge \vec{v} = \begin{pmatrix}y_1z_2-z_1y_2\\z_1x_2-x_1z_2\\x_1y_2-y_1x_2\end{pmatrix}\) |
| Norme | \(\|\vec{u}\| = \sqrt{x^2 + y^2 + z^2}\) |
| Angle | \(\cos(\theta) = \frac{\vec{u} \cdot \vec{v}}{\|\vec{u}\| \|\vec{v}\|}\) |
| Type | Formule |
|---|---|
| Point-Point | \(d = \|\overrightarrow{AB}\|\) |
| Point-Plan | \(d = \frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\) |
| Point-Droite | \(d = \frac{\|\overrightarrow{AM} \wedge \vec{u}\|}{\|\vec{u}\|}\) |
| Droites gauches | \(d = \frac{|\overrightarrow{A_1A_2} \cdot (\vec{u_1} \wedge \vec{u_2})|}{\|\vec{u_1} \wedge \vec{u_2}\|}\) |
🎓 Géométrie dans l'espace - Cours complet
Maîtrisez les concepts fondamentaux pour réussir vos examens et applications pratiques
Déterminer l'équation cartésienne du plan passant par les points \(M_1(1, 2, 3)\), \(M_2(4, -1, 2)\) et \(M_3(0, 1, 5)\).
Soit le plan \(P\) d'équation cartésienne \(3x - 2y + z - 5 = 0\) et le point \(A(2, 1, 4)\).
Calculer la distance du point \(A\) au plan \(P\), notée \(d(A, P)\).
Soient \(A(x_0; y_0; z_0)\) et \(P\) le plan d'équation \(ax+by+cz+d= 0\). Demontrer que la distance du point \(A\) au plan \(P\), notée \(d(A, P)\), vérifie:\[d(A,P) = \frac{\lvert ax_0 + by_0 + cz_0 + d \rvert}{\sqrt{a^2 + b^2 + c^2}}\]
Soient deux plans \(P_1\) et \(P_2\) d'équations respectives :
\(P_1 : 2x + 3y - z = 5\)
\(P_2 : x - 2y + 4z = 8\)
1. Déterminer l'équation de la droite d'intersection des deux plans.
2. Trouver un point appartenant à cette droite d'intersection.
Soit une droite \(D\) d'équation paramétrique :
\(D : r(t) = (2, -1, 3) + t(1, 2, -1)\)
Et un plan \(P\) d'équation :
\(P : 3x - y + 2z = 7\)
1. Déterminer l'équation cartésienne de la droite \(D\).
2. Trouver les coordonnées du point d'intersection de la droite \(D\) et du plan \(P\).
Soient trois plans \(P_1\), \(P_2\) et \(P_3\) d'équations respectives :
\(P_1 : x + y - z = 1\)
\(P_2 : 2x - y + 3z = 5\)
\(P_3 : 3x + 2y + z = 7\)
Déterminer les coordonnées du point d'intersection des trois plans.
Dans l'espace tridimensionnel, une droite est définie par un point et un vecteur directeur. Une droite D passant par le point \(A(x_0, y_0, z_0)\) et dirigée par le vecteur \(\vec{u}\begin{pmatrix}a\\b\\c\end{pmatrix}\) admet pour équation paramétrique :
Le paramètre \(t\) parcourt l'ensemble des nombres réels, permettant d'obtenir tous les points de la droite.
Exemple : Droite passant par \(A(1, -2, 3)\) et dirigée par \(\vec{u}\begin{pmatrix}2\\1\\-1\end{pmatrix}\) :
Pour deux points distincts \(A(x_1,y_1,z_1)\) et \(B(x_2,y_2,z_2)\), le vecteur directeur est : \(\vec{AB} = \begin{pmatrix}x_2-x_1\\y_2-y_1\\z_2-z_1\end{pmatrix}\)
Lorsque les composantes du vecteur directeur sont toutes non nulles, on peut écrire :
Figure 1 : Représentation paramétrique d'une droite dans l'espace
L'intersection d'une droite et d'un plan se détermine en substituant les équations paramétriques de la droite dans l'équation du plan.
Soit :
Étape 1 : Substituer les équations de D dans P.
Étape 2 : Regrouper et résoudre pour \(t\).
Si \(\vec{u} \cdot \vec{n} = Aa + Bb + Cc \neq 0\), alors il existe un unique point d'intersection :
Si \(\vec{u} \cdot \vec{n} = 0\) (vecteur directeur orthogonal au vecteur normal) :
Figure 2 : Intersection droite-plan : cas sécant et parallèle
Dans l'espace, deux droites peuvent être coplanaires (dans le même plan) ou gauches (non coplanaires).
Soit deux droites définies par :
\(D_1\): \(\vec{OM} = \vec{OA} + t \cdot \vec{u}\) \((t \in \mathbb{R})\)
\(D_2\): \(\vec{OM} = \vec{OB} + s \cdot \vec{v}\) \((s \in \mathbb{R})\)
Condition nécessaire d'intersection : Les droites sont coplanaires si et seulement si :
Cette condition signifie que les vecteurs \(\vec{AB}\), \(\vec{u}\) et \(\vec{v}\) sont coplanaires.
Si les droites se coupent, il existe \(t_0\) et \(s_0\) tels que :
Ce qui donne le système : \(\vec{AB} = s_0 \vec{v} - t_0 \vec{u}\)
Figure 3 : Intersection de deux droites coplanaires
Deux plans non parallèles dans l'espace se coupent suivant une droite.
Soit deux plans :
\(P_1\): \(a_1x + b_1y + c_1z = d_1\)
\(P_2\): \(a_2x + b_2y + c_2z = d_2\)
Droite d'intersection : L'ensemble des points \((x,y,z)\) vérifiant simultanément les deux équations.
Vecteur directeur : \(\vec{u} = \vec{n_1} \wedge \vec{n_2}\)
où \(\vec{n_1}(a_1, b_1, c_1)\) et \(\vec{n_2}(a_2, b_2, c_2)\) sont les vecteurs normaux aux plans.
L'intersection de trois plans présente plusieurs cas selon le rang du système d'équations.
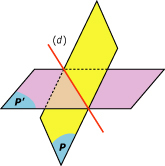
Figure 4 : Intersection de deux plans rectangulaires formant une droite D
Pour résoudre un problème d'intersection :
Trouver l'intersection de la droite \(D\) et du plan \(P\) :
\(D\): \(\begin{cases} x = 1 + 2t \\ y = -1 + t \\ z = 3 - t \end{cases}\)
\(P\): \(x + 2y - z + 4 = 0\)
Solution : Substitution dans l'équation du plan :
\((1 + 2t) + 2(-1 + t) - (3 - t) + 4 = 0\)
\(1 + 2t - 2 + 2t - 3 + t + 4 = 0\)
\(5t = 0 \Rightarrow t = 0\)
Point d'intersection : \(I(1, -1, 3)\)
Pour deux droites gauches \(D_1\) et \(D_2\), la distance est :
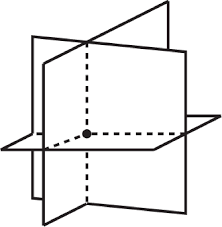
Figure 5 : Intersection de trois plans en un point
Déterminer l'équation cartésienne du plan passant par les points \(A(1, 2, 3)\), \(B(2, 1, 4)\) et \(C(3, 4, -1)\).
Déterminer l'équation paramétrique de la droite passant par le point \(A(1, 2, 3)\) et parallèle au vecteur directeur \(\vec{d} = (2, -1, 4)\).
Déterminer l'équation cartésienne du plan passant par l'origine et parallèle aux vecteurs \((1, 2, 3)\) et \((4, -1, 2)\).
Soient les plans \(P_1 : 2x + 3y - z + 4 = 0\) et \(P_2 : 4x - 6y + 2z - 8 = 0\). Déterminer la position relative de ses deux plans.
Soient les droites \(d_1 : \begin{cases} x = 2 + 4t \\ y = 1 + 2t \\ z = 3 + 5t \end{cases}\) et \(d_2 : \begin{cases} x = 3 - t \\ y = 3 - 2t \\ z = 7 - 5t \end{cases}\). Déterminer la position relative de ces deux droites.
Soient les droites \(d_1 : x = 1 + 3t, y = 2 + 3t, z = 3 + 3t\) et \(d_2 : x = t, y = 3 + t, z = 1 + 3t\). Déterminer la position relative de ses deux droites.
Soit la droite \(d : x = 1 + 2t, y = 3 - t, z = 2 + 3t\) et le plan \(P : 3x - 2y + z - 5 = 0\). Déterminer la position relative d'une droite \(d\) et du plan \(P\).
Définition : Le projeté orthogonal d'un point M sur un plan Π est le point H ∈ Π tel que MH ⊥ Π.
Méthode pratique :
Soient deux droites :
Méthode :
Soient deux plans :
Méthode pour trouver la droite :
Soit :
Calcul du point :
Figure : Visualisation des projections et intersections dans l'espace
Énoncé : Soit le plan Π : 2x - y + 3z = 6 et le point M(1, -2, 4).
La géométrie dans l'espace ℝ³ nécessite des outils précis pour décrire les positions et les relations entre les objets géométriques. Trois concepts fondamentaux structurent cette approche : les points qui définissent des positions exactes, les vecteurs qui caractérisent les déplacements et les directions, et les repères qui établissent un système de référence absolu.
Une base vectorielle \((\vec{i}, \vec{j}, \vec{k})\) peut présenter différentes propriétés géométriques importantes :
Règle de la main droite : En plaçant le pouce selon \(\vec{i}\), l'index selon \(\vec{j}\), le majeur doit pointer naturellement selon \(\vec{k}\) pour former un trièdre direct.
Dans un repère \((O, \vec{i}, \vec{j}, \vec{k})\), tout point M de l'espace peut être repéré de manière unique par ses coordonnées \((x, y, z)\) telles que :
\(\overrightarrow{OM} = x\vec{i} + y\vec{j} + z\vec{k}\)
Les principales propriétés métriques sont :
Figure 1 : Représentation d'un repère orthonormé direct dans l'espace
Une famille de trois vecteurs \((\vec{u}, \vec{v}, \vec{w})\) forme une base de ℝ³ si et seulement si ces vecteurs sont linéairement indépendants. Cela signifie que la seule solution à l'équation vectorielle :
\(a\vec{u} + b\vec{v} + c\vec{w} = \vec{0}\)
est la solution triviale : \(a = b = c = 0\).
1. Méthode du déterminant :
Soit \(\vec{u}(x_1, y_1, z_1)\), \(\vec{v}(x_2, y_2, z_2)\), \(\vec{w}(x_3, y_3, z_3)\).
Les vecteurs forment une base si et seulement si :
\(\det(\vec{u}, \vec{v}, \vec{w}) = \begin{vmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{vmatrix} \neq 0\)
2. Méthode par résolution de système :
Résoudre \(a\vec{u} + b\vec{v} + c\vec{w} = \vec{0}\) et vérifier que \(a = b = c = 0\) est la seule solution.
3. Méthode géométrique :
Vérifier que les trois vecteurs ne sont pas coplanaires.
Question : Les vecteurs \(\vec{u}(1, 2, 1)\), \(\vec{v}(2, 1, 0)\) et \(\vec{w}(1, 0, 2)\) forment-ils une base de ℝ³ ?
Solution par déterminant :
Calculons le déterminant :
\(\det(\vec{u}, \vec{v}, \vec{w}) = \begin{vmatrix} 1 & 2 & 1 \\ 2 & 1 & 0 \\ 1 & 0 & 2 \end{vmatrix}\)
Développement selon la première ligne :
\(= 1 \cdot \begin{vmatrix} 1 & 0 \\ 0 & 2 \end{vmatrix} - 2 \cdot \begin{vmatrix} 2 & 0 \\ 1 & 2 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & 1 \\ 1 & 0 \end{vmatrix}\)
\(= 1 \cdot (1 \cdot 2 - 0 \cdot 0) - 2 \cdot (2 \cdot 2 - 0 \cdot 1) + 1 \cdot (2 \cdot 0 - 1 \cdot 1)\)
\(= 1 \cdot 2 - 2 \cdot 4 + 1 \cdot (-1) = 2 - 8 - 1 = -7\)
Conclusion : Puisque \(\det(\vec{u}, \vec{v}, \vec{w}) = -7 \neq 0\), les trois vecteurs forment bien une base de ℝ³.
Figure 2 : Comparaison entre une base valide et des vecteurs coplanaires
Un quadruplet \((O, \vec{u}, \vec{v}, \vec{w})\) forme un repère de l'espace si et seulement si :
La condition essentielle est donc que les trois vecteurs soient linéairement indépendants.
Pour vérifier qu'un quadruplet forme un repère, il suffit de :
Cas particuliers importants :
Question : Le quadruplet \((A, \vec{AB}, \vec{AC}, \vec{AD})\) forme-t-il un repère, sachant que :
Solution :
Calculons les vecteurs :
Calculons le déterminant :
\(\det(\vec{AB}, \vec{AC}, \vec{AD}) = \begin{vmatrix} 1 & -1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \end{vmatrix}\)
Développement selon la première ligne :
\(= 1 \cdot \begin{vmatrix} 1 & 1 \\ 1 & 2 \end{vmatrix} - (-1) \cdot \begin{vmatrix} 1 & 1 \\ 0 & 2 \end{vmatrix} + 0 \cdot \begin{vmatrix} 1 & 1 \\ 0 & 1 \end{vmatrix}\)
\(= 1 \cdot (2 - 1) + 1 \cdot (2 - 0) = 1 + 2 = 3\)
Conclusion : Puisque \(\det(\vec{AB}, \vec{AC}, \vec{AD}) = 3 \neq 0\), le quadruplet \((A, \vec{AB}, \vec{AC}, \vec{AD})\) forme bien un repère de l'espace.
Figure 3 : Représentation géométrique d'un repère formé par quatre points
Énoncé : Soit ℛ\((O,\vec{i},\vec{j},\vec{k})\) un repère orthonormé direct. Déterminer si les vecteurs \(\vec{u} = \vec{i} + 2\vec{j} - \vec{k}\), \(\vec{v} = 2\vec{i} - \vec{j} + 3\vec{k}\) et \(\vec{w} = \vec{i} + \vec{j} + \vec{k}\) forment une base de ℝ³.
Solution :
Exprimons les vecteurs dans la base canonique :
Calculons le déterminant :
\(\det(\vec{u}, \vec{v}, \vec{w}) = \begin{vmatrix} 1 & 2 & 1 \\ 2 & -1 & 1 \\ -1 & 3 & 1 \end{vmatrix}\)
Développement selon la première ligne :
\(= 1 \cdot \begin{vmatrix} -1 & 1 \\ 3 & 1 \end{vmatrix} - 2 \cdot \begin{vmatrix} 2 & 1 \\ -1 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & -1 \\ -1 & 3 \end{vmatrix}\)
\(= 1 \cdot (-1 - 3) - 2 \cdot (2 + 1) + 1 \cdot (6 - 1)\)
\(= -4 - 6 + 5 = -5\)
Conclusion : \(\det(\vec{u}, \vec{v}, \vec{w}) = -5 \neq 0\), donc les trois vecteurs forment bien une base de ℝ³.
Énoncé : Soit A(1,0,1), B(2,1,0), C(0,1,2) et D(1,1,1). Le repère \((A, \vec{AB}, \vec{AC}, \vec{AD})\) est-il orthogonal ?
Solution :
Calculons les vecteurs :
Vérifions l'orthogonalité deux à deux :
Conclusion : Le repère n'est pas orthogonal car \(\vec{AB} \cdot \vec{AC} \neq 0\).
Énoncé : Dans le repère \((O, \vec{i}, \vec{j}, \vec{k})\), soit M(2,3,1). Calculer les coordonnées de M dans le repère \((O, \vec{u}, \vec{v}, \vec{w})\) où \(\vec{u} = \vec{i} + \vec{j}\), \(\vec{v} = \vec{i} - \vec{j}\), \(\vec{w} = \vec{k}\).
Solution :
Il faut exprimer \(\overrightarrow{OM} = 2\vec{i} + 3\vec{j} + \vec{k}\) dans la base \((\vec{u}, \vec{v}, \vec{w})\).
Cherchons \(a, b, c\) tels que :
\(2\vec{i} + 3\vec{j} + \vec{k} = a\vec{u} + b\vec{v} + c\vec{w}\)
En substituant :
\(2\vec{i} + 3\vec{j} + \vec{k} = a(\vec{i} + \vec{j}) + b(\vec{i} - \vec{j}) + c\vec{k}\)
Par identification des coefficients :
Résolution du système :
D'où : \(a = \frac{5}{2}\), \(b = -\frac{1}{2}\), \(c = 1\)
Conclusion : Les coordonnées de M dans le repère \((O, \vec{u}, \vec{v}, \vec{w})\) sont \(\left(\frac{5}{2}, -\frac{1}{2}, 1\right)\).
Figure 4 : Même point, coordonnées différentes selon la base
Pour vérifier qu'une famille forme une base :
Pour vérifier qu'un quadruplet forme un repère :
La géométrie dans l'espace ℝ³ nécessite des outils précis pour décrire les positions et les relations entre les objets géométriques. Trois concepts fondamentaux structurent cette approche : les points qui définissent des positions exactes, les vecteurs qui caractérisent les déplacements et les directions, et les repères qui établissent un système de référence absolu.
Une base vectorielle \((\vec{i}, \vec{j}, \vec{k})\) peut présenter différentes propriétés géométriques importantes :
Règle de la main droite : En plaçant le pouce selon \(\vec{i}\), l'index selon \(\vec{j}\), le majeur doit pointer naturellement selon \(\vec{k}\) pour former un trièdre direct.
Dans un repère \((O, \vec{i}, \vec{j}, \vec{k})\), tout point M de l'espace peut être repéré de manière unique par ses coordonnées \((x, y, z)\) telles que :
\(\overrightarrow{OM} = x\vec{i} + y\vec{j} + z\vec{k}\)
Les principales propriétés métriques sont :
Figure 1 : Représentation d'un repère orthonormé direct dans l'espace
Une famille de trois vecteurs \((\vec{u}, \vec{v}, \vec{w})\) forme une base de ℝ³ si et seulement si ces vecteurs sont linéairement indépendants. Cela signifie que la seule solution à l'équation vectorielle :
\(a\vec{u} + b\vec{v} + c\vec{w} = \vec{0}\)
est la solution triviale : \(a = b = c = 0\).
1. Méthode du déterminant :
Soit \(\vec{u}(x_1, y_1, z_1)\), \(\vec{v}(x_2, y_2, z_2)\), \(\vec{w}(x_3, y_3, z_3)\).
Les vecteurs forment une base si et seulement si :
\(\det(\vec{u}, \vec{v}, \vec{w}) = \begin{vmatrix} x_1 & x_2 & x_3 \\ y_1 & y_2 & y_3 \\ z_1 & z_2 & z_3 \end{vmatrix} \neq 0\)
2. Méthode par résolution de système :
Résoudre \(a\vec{u} + b\vec{v} + c\vec{w} = \vec{0}\) et vérifier que \(a = b = c = 0\) est la seule solution.
3. Méthode géométrique :
Vérifier que les trois vecteurs ne sont pas coplanaires.
Question : Les vecteurs \(\vec{u}(1, 2, 1)\), \(\vec{v}(2, 1, 0)\) et \(\vec{w}(1, 0, 2)\) forment-ils une base de ℝ³ ?
Solution par déterminant :
Calculons le déterminant :
\(\det(\vec{u}, \vec{v}, \vec{w}) = \begin{vmatrix} 1 & 2 & 1 \\ 2 & 1 & 0 \\ 1 & 0 & 2 \end{vmatrix}\)
Développement selon la première ligne :
\(= 1 \cdot \begin{vmatrix} 1 & 0 \\ 0 & 2 \end{vmatrix} - 2 \cdot \begin{vmatrix} 2 & 0 \\ 1 & 2 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & 1 \\ 1 & 0 \end{vmatrix}\)
\(= 1 \cdot (1 \cdot 2 - 0 \cdot 0) - 2 \cdot (2 \cdot 2 - 0 \cdot 1) + 1 \cdot (2 \cdot 0 - 1 \cdot 1)\)
\(= 1 \cdot 2 - 2 \cdot 4 + 1 \cdot (-1) = 2 - 8 - 1 = -7\)
Conclusion : Puisque \(\det(\vec{u}, \vec{v}, \vec{w}) = -7 \neq 0\), les trois vecteurs forment bien une base de ℝ³.
Figure 2 : Comparaison entre une base valide et des vecteurs coplanaires
Un quadruplet \((O, \vec{u}, \vec{v}, \vec{w})\) forme un repère de l'espace si et seulement si :
La condition essentielle est donc que les trois vecteurs soient linéairement indépendants.
Pour vérifier qu'un quadruplet forme un repère, il suffit de :
Cas particuliers importants :
Question : Le quadruplet \((A, \vec{AB}, \vec{AC}, \vec{AD})\) forme-t-il un repère, sachant que :
Solution :
Calculons les vecteurs :
Calculons le déterminant :
\(\det(\vec{AB}, \vec{AC}, \vec{AD}) = \begin{vmatrix} 1 & -1 & 0 \\ 1 & 1 & 1 \\ 0 & 1 & 2 \end{vmatrix}\)
Développement selon la première ligne :
\(= 1 \cdot \begin{vmatrix} 1 & 1 \\ 1 & 2 \end{vmatrix} - (-1) \cdot \begin{vmatrix} 1 & 1 \\ 0 & 2 \end{vmatrix} + 0 \cdot \begin{vmatrix} 1 & 1 \\ 0 & 1 \end{vmatrix}\)
\(= 1 \cdot (2 - 1) + 1 \cdot (2 - 0) = 1 + 2 = 3\)
Conclusion : Puisque \(\det(\vec{AB}, \vec{AC}, \vec{AD}) = 3 \neq 0\), le quadruplet \((A, \vec{AB}, \vec{AC}, \vec{AD})\) forme bien un repère de l'espace.
Figure 3 : Représentation géométrique d'un repère formé par quatre points
Énoncé : Soit ℛ\((O,\vec{i},\vec{j},\vec{k})\) un repère orthonormé direct. Déterminer si les vecteurs \(\vec{u} = \vec{i} + 2\vec{j} - \vec{k}\), \(\vec{v} = 2\vec{i} - \vec{j} + 3\vec{k}\) et \(\vec{w} = \vec{i} + \vec{j} + \vec{k}\) forment une base de ℝ³.
Solution :
Exprimons les vecteurs dans la base canonique :
Calculons le déterminant :
\(\det(\vec{u}, \vec{v}, \vec{w}) = \begin{vmatrix} 1 & 2 & 1 \\ 2 & -1 & 1 \\ -1 & 3 & 1 \end{vmatrix}\)
Développement selon la première ligne :
\(= 1 \cdot \begin{vmatrix} -1 & 1 \\ 3 & 1 \end{vmatrix} - 2 \cdot \begin{vmatrix} 2 & 1 \\ -1 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & -1 \\ -1 & 3 \end{vmatrix}\)
\(= 1 \cdot (-1 - 3) - 2 \cdot (2 + 1) + 1 \cdot (6 - 1)\)
\(= -4 - 6 + 5 = -5\)
Conclusion : \(\det(\vec{u}, \vec{v}, \vec{w}) = -5 \neq 0\), donc les trois vecteurs forment bien une base de ℝ³.
Énoncé : Soit A(1,0,1), B(2,1,0), C(0,1,2) et D(1,1,1). Le repère \((A, \vec{AB}, \vec{AC}, \vec{AD})\) est-il orthogonal ?
Solution :
Calculons les vecteurs :
Vérifions l'orthogonalité deux à deux :
Conclusion : Le repère n'est pas orthogonal car \(\vec{AB} \cdot \vec{AC} \neq 0\).
Énoncé : Dans le repère \((O, \vec{i}, \vec{j}, \vec{k})\), soit M(2,3,1). Calculer les coordonnées de M dans le repère \((O, \vec{u}, \vec{v}, \vec{w})\) où \(\vec{u} = \vec{i} + \vec{j}\), \(\vec{v} = \vec{i} - \vec{j}\), \(\vec{w} = \vec{k}\).
Solution :
Il faut exprimer \(\overrightarrow{OM} = 2\vec{i} + 3\vec{j} + \vec{k}\) dans la base \((\vec{u}, \vec{v}, \vec{w})\).
Cherchons \(a, b, c\) tels que :
\(2\vec{i} + 3\vec{j} + \vec{k} = a\vec{u} + b\vec{v} + c\vec{w}\)
En substituant :
\(2\vec{i} + 3\vec{j} + \vec{k} = a(\vec{i} + \vec{j}) + b(\vec{i} - \vec{j}) + c\vec{k}\)
Par identification des coefficients :
Résolution du système :
D'où : \(a = \frac{5}{2}\), \(b = -\frac{1}{2}\), \(c = 1\)
Conclusion : Les coordonnées de M dans le repère \((O, \vec{u}, \vec{v}, \vec{w})\) sont \(\left(\frac{5}{2}, -\frac{1}{2}, 1\right)\).
Figure 4 : Même point, coordonnées différentes selon la base
Pour vérifier qu'une famille forme une base :
Pour vérifier qu'un quadruplet forme un repère :
Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !