Exploration des arbres binaires de recherche (ABR)
Un arbre binaire de recherche (ABR) est un type particulier d'arbre binaire où les valeurs des nœuds sont organisées de manière à permettre une recherche efficace. Pour chaque nœud de l'ABR, toutes les valeurs dans son sous-arbre gauche sont inférieures à sa valeur, et toutes les valeurs dans son sous-arbre droit sont supérieures à sa valeur.
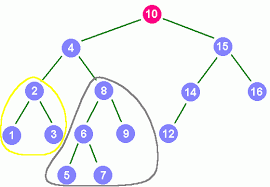
En Python, un ABR peut être représenté en utilisant une classe Noeud similaire à celle utilisée pour les arbres binaires, mais avec quelques modifications pour respecter les propriétés des ABR. Voici une implémentation de base :
class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.gauche = None
self.droit = None
L'opération d'insertion dans un ABR consiste à ajouter un nœud contenant une valeur donnée tout en maintenant les propriétés de l'ABR. Voici comment implémenter cette opération en Python :
def inserer_noeud(racine, valeur):
if racine is None:
return Noeud(valeur)
if valeur < racine.valeur:
racine.gauche = inserer_noeud(racine.gauche, valeur)
else:
racine.droit = inserer_noeud(racine.droit, valeur)
return racine
L'opération de recherche dans un ABR consiste à trouver le nœud contenant une valeur donnée. Voici comment implémenter cette opération en Python :
def rechercher_noeud(racine, valeur):
if racine is None or racine.valeur == valeur::
return racine
if valeur < racine.valeur:
return rechercher_noeud(racine.gauche, valeur)
else:
return rechercher_noeud(racine.droit, valeur)
Les parcours d'arbres binaires mentionnés dans la fiche précédente (parcours préfixe, infixe et postfixe) peuvent également être appliqués aux ABR. Cependant, en raison de la propriété d'ordonnancement des valeurs, le parcours infixe d'un ABR renvoie les valeurs triées par ordre croissant.
Voici comment implémenter les parcours dans un ABR en Python :
def parcours_prefixe(racine):
if racine is not None:
print(racine.valeur)
parcours_prefixe(racine.gauche)
parcours_prefixe(racine.droit)
def parcours_infixe(racine):
if racine is not None:
parcours_infixe(racine.gauche)
print(racine.valeur)
parcours_infixe(racine.droit)
def parcours_postfixe(racine):
if racine is not None:
parcours_postfixe(racine.gauche)
parcours_postfixe(racine.droit)
print(racine.valeur)
Supposons que nous voulions créer un ABR contenant les valeurs suivantes : [5, 3, 7, 2, 4, 6, 8]. Voici comment créer cet ABR à l'aide de l'opération d'insertion :
valeurs = [5, 3, 7, 2, 4, 6, 8]
racine = None
for valeur in valeurs:
racine = inserer_noeud(racine, valeur)Maintenant, nous pouvons effectuer différentes opérations sur cet ABR, par exemple rechercher un nœud contenant une valeur donnée :
valeur_recherchee = 4
noeud_recherche = rechercher_noeud(racine, valeur_recherchee)
if noeud_recherche is not None:
print("Noeud trouvé : ", noeud_recherche.valeur)
else:
print("Noeud non trouvé.")Nous pouvons égalementpoursuivre en effectuant des parcours dans l'ABR :
print("Parcours préfixe :")
parcours_prefixe(racine)
print("Parcours infixe (valeurs triées) :")
parcours_infixe(racine)
print("Parcours postfixe :")
parcours_postfixe(racine)Cela affichera le résultat suivant :
Parcours préfixe :
5
3
2
4
7
6
8
Parcours infixe (valeurs triées) :
2
3
4
5
6
7
8
Parcours postfixe :
2
4
3
6
8
7
5L'opération de suppression dans un ABR consiste à retirer un nœud contenant une valeur donnée tout en maintenant les propriétés de l'ABR. La suppression dans un ABR peut être un peu plus complexe, car elle doit prendre en compte plusieurs cas différents (par exemple, le nœud à supprimer a zéro, un ou deux enfants).
Voici un exemple d'implémentation de l'opération de suppression :
def supprimer_noeud(racine, valeur):
if racine is None:
return racine
if valeur < racine.valeur:
racine.gauche = supprimer_noeud(racine.gauche, valeur)
elif valeur > racine.valeur:
racine.droit = supprimer_noeud(racine.droit, valeur)
else:
# Cas où le nœud à supprimer a zéro ou un enfant
if racine.gauche is None:
return racine.droit
elif racine.droit is None:
return racine.gauche
# Cas où le nœud à supprimer a deux enfants
successeur = trouver_successeur(racine.droit)
racine.valeur = successeur.valeur
racine.droit = supprimer_noeud(racine.droit, successeur.valeur)
return racine
Dans cette implémentation, la fonction trouver_successeur est utilisée pour trouver la valeur successeur (la plus petite valeur plus grande que la valeur du nœud à supprimer) dans le sous-arbre droit du nœud à supprimer.
Le codage de Huffman est une technique de compression de données sans perte. Voici quelques exemples pratiques pour vous aider à comprendre comment réaliser le codage de Huffman en Python.
Supposons que nous ayons les symboles suivants avec leurs fréquences d'apparition :
| Symbole | Fréquence |
|---|---|
| A | 4 |
| B | 2 |
| C | 1 |
| D | 1 |
[('C', 1), ('D', 1), ('B', 2), ('A', 4)]
[('B', 2), ('A', 4), ('C', 1, 'D', 1)]
[('A', 4), ('C', 1, 'D', 1, 'B', 2)]
[('C', 1, 'D', 1, 'B', 2, 'A', 4)]
Root
/ \
7 / \ 4
/ \
C:1 D:1 B:2 A:4| Symbole | Fréquence |
|---|---|
| A | 0 |
| B | 10 |
| C | 110 |
| D | 111 |
message = "ABACADABRA"
message_compressé = "0100110110000110101101"
message_compressé = "0100110110000110101101"
message_décompressé = "ABACADABRA"
Les arbres binaires de recherche sont une extension importante des arbres binaires, offrant des opérations de recherche efficaces sur des ensembles de données ordonnées. La compréhension de leur structure et de leurs opérations clés est essentielle pour de nombreux problèmes et algorithmes.
Écrivez une fonction Python qui compte le nombre total de nœuds dans un arbre binaire.
La fonction compter_noeuds utilise une approche récursive pour parcourir l'arbre et compter le nombre total de nœuds. Lorsque l'arbre est vide (None), la fonction renvoie 0. Sinon, elle renvoie 1 plus la somme du nombre de nœuds dans le sous-arbre gauche et le sous-arbre droit.
class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.gauche = None
self.droite = None
def compter_noeuds(arbre):
if arbre is None:
return 0
return 1 + compter_noeuds(arbre.gauche) + compter_noeuds(arbre.droite)
# Exemple d'utilisation
arbre = Noeud(1)
arbre.gauche = Noeud(2)
arbre.droite = Noeud(3)
arbre.gauche.gauche = Noeud(4)
arbre.gauche.droite = Noeud(5)
print(compter_noeuds(arbre)) # Résultat attendu: 5
Écrivez une fonction Python qui vérifie si un arbre binaire est un arbre binaire de recherche (ABR) valide.
La fonction est_abr_valide utilise une approche récursive pour vérifier si un arbre binaire est un arbre binaire de recherche (ABR) valide. Elle prend en compte les valeurs minimales et maximales autorisées pour chaque nœud de l'arbre. Si la valeur d'un nœud est inférieure ou égale à la valeur minimale autorisée ou supérieure ou égale à la valeur maximale autorisée, l'ABR n'est pas valide. La fonction renvoie True si toutes les sous-arbres sont des ABR valides et False sinon.
class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.gauche = None
self.droite = None
def est_abr_valide(arbre, min_val=float('-inf'), max_val=float('inf')):
if arbre is None:
return True
if arbre.valeur <= min_val or arbre.valeur >= max_val:
return False
return (est_abr_valide(arbre.gauche, min_val, arbre.valeur) and
est_abr_valide(arbre.droite, arbre.valeur, max_val))
# Exemple d'utilisation
arbre = Noeud(4)
arbre.gauche = Noeud(2)
arbre.droite = Noeud(6)
arbre.gauche.gauche = Noeud(1)
arbre.gauche.droite = Noeud(3)
arbre.droite.gauche = Noeud(5)
arbre.droite.droite = Noeud(7)
print(est_abr_valide(arbre)) # Résultat attendu: True
Écrivez une fonction Python qui calcule la hauteur d'un arbre binaire.
La fonction hauteur_arbre utilise une approche récursive pour calculer la hauteur d'un arbre binaire. La hauteur d'un arbre vide est définie comme 0, et la hauteur d'un arbre non vide est calculée comme la plus grande hauteur entre le sous-arbre gauche et le sous-arbre droit, plus 1.
class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.gauche = None
self.droite = None
def hauteur_arbre(arbre):
if arbre is None:
return 0
hauteur_gauche = hauteur_arbre(arbre.gauche)
hauteur_droite = hauteur_arbre(arbre.droite)
return max(hauteur_gauche, hauteur_droite) + 1
# Exemple d'utilisation
arbre = Noeud(1)
arbre.gauche = Noeud(2)
arbre.droite = Noeud(3)
arbre.gauche.gauche = Noeud(4)
arbre.gauche.droite = Noeud(5)
arbre.droite.droite = Noeud(6)
print(hauteur_arbre(arbre)) # Résultat attendu: 3
Écrivez une fonction Python qui effectue un parcours en profondeur préfixe d'un arbre binaire et renvoie une liste contenant les valeurs des nœuds visités.
class Noeud:
def __init__(self, valeur):
self.valeur = valeur
self.gauche = None
self.droite = None
def parcours_prefixe(arbre):
if arbre is None:
return []
return [arbre.valeur] + parcours_prefixe(arbre.gauche) + parcours_prefixe(arbre.droite)
# Exemple d'utilisation
arbre = Noeud(1)
arbre.gauche = Noeud(2)
arbre.droite = Noeud(3)
arbre.gauche.gauche = Noeud(4)
arbre.gauche.droite = Noeud(5)
print(parcours_prefixe(arbre)) # Résultat attendu: [1, 2, 4, 5, 3]
parcours_prefixe utilise une approche récursive pour effectuer un parcours en profondeur préfixe d'un arbre binaire. L'algorithme visite d'abord la racine, puis effectue le parcours en profondeur préfixe du sous-arbre gauche, suivi du parcours en profondeur préfixe du sous-arbre droit. Les valeurs des nœuds visités sont ajoutées à une liste qui est renvoyée à la fin.
Considérez l'arbre binaire suivant :
5
/ \
3 7
/ \ / \
1 4 6 9
a) Parcourez cet arbre en utilisant le parcours préfixe (préordre).
Solution : 5, 3, 1, 4, 7, 6, 9
b) Parcourez cet arbre en utilisant le parcours infixe (inordre).
Solution : 1, 3, 4, 5, 6, 7, 9
c) Parcourez cet arbre en utilisant le parcours postfixe (postordre).
Solution : 1, 4, 3, 6, 9, 7, 5
Considérez l'arbre binaire suivant :
A
/ \
B C
/ \ / \
D E F G
a) Quel est le niveau de l'arbre où se trouve le nœud D ?
Solution : Le niveau du nœud D est 2.
b) Quels sont les nœuds frères dans cet arbre ?
Solution : Les nœuds frères sont B et C.
c) Quel est le nœud parent du nœud E ?
Solution : Le nœud parent du nœud E est B.
Créez une classe Node pour représenter un nœud dans un arbre binaire. Chaque nœud doit avoir une valeur et des références vers ses nœuds enfants gauche et droit.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = NoneImplémentez une fonction insert qui prend en paramètre un nœud root et une valeur, et insère cette valeur dans l'arbre binaire de recherche correspondant. Assurez-vous que les valeurs plus petites sont insérées à gauche et les valeurs plus grandes à droite.
def insert(root, value):
if root is None:
return Node(value)
if value < root.value:
root.left = insert(root.left, value)
else:
root.right = insert(root.right, value)
return rootImplémentez une fonction récursive preorder_traversal qui prend en paramètre un nœud root et effectue un parcours préfixe (préordre) de l'arbre en imprimant les valeurs des nœuds.
def preorder_traversal(root):
if root is not None:
print(root.value, end=" ")
preorder_traversal(root.left)
preorder_traversal(root.right)Implémentez une fonction récursive search qui prend en paramètre un nœud root et une valeur, et recherche cette valeur dans l'arbre binaire. La fonction doit renvoyer True si la valeur est présente et False sinon.
def search(root, value):
if root is None or root.value == value:
return root is not None
if value < root.value:
return search(root.left, value)
else:
return search(root.right, value)Considérez l'arbre binaire suivant :
A
/ \
B C
/ \ / \
D E F G
a) Quel est le niveau de l'arbre où se trouve le nœud D ?
Solution : Le niveau du nœud D est 2.
b) Quels sont les nœuds frères dans cet arbre ?
Solution : Les nœuds frères sont B et C.
c) Quel est le nœud parent du nœud E ?
Solution : Le nœud parent du nœud E est B.
Créez une classe Node pour représenter un nœud dans un arbre binaire. Chaque nœud doit avoir une valeur et des références vers ses nœuds enfants gauche et droit.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = NoneImplémentez une fonction insert qui prend en paramètre un nœud root et une valeur, et insère cette valeur dans l'arbre binaire de recherche correspondant. Assurez-vous que les valeurs plus petites sont insérées à gauche et les valeurs plus grandes à droite.
def insert(root, value):
if root is None:
return Node(value)
if value < root.value:
root.left = insert(root.left, value)
else:
root.right = insert(root.right, value)
return rootImplémentez une fonction récursive preorder_traversal qui prend en paramètre un nœud root et effectue un parcours préfixe (préordre) de l'arbre en imprimant les valeurs des nœuds.
def preorder_traversal(root):
if root is not None:
print(root.value, end=" ")
preorder_traversal(root.left)
preorder_traversal(root.right)Implémentez une fonction récursive search qui prend en paramètre un nœud root et une valeur, et recherche cette valeur dans l'arbre binaire. La fonction doit renvoyer True si la valeur est présente et False sinon.
def search(root, value):
if root is None or root.value == value:
return root is not None
if value < root.value:
return search(root.left, value)
else:
return search(root.right, value)Considérez l'arbre binaire suivant :
A
/ \
B C
/ \ / \
D E F G
a) Quel est le niveau de l'arbre où se trouve le nœud D ?
Solution : Le niveau du nœud D est 2.
b) Quels sont les nœuds frères dans cet arbre ?
Solution : Les nœuds frères sont B et C.
c) Quel est le nœud parent du nœud E ?
Solution : Le nœud parent du nœud E est B.
Créez une classe Node pour représenter un nœud dans un arbre binaire. Chaque nœud doit avoir une valeur et des références vers ses nœuds enfants gauche et droit.
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = NoneImplémentez une fonction insert qui prend en paramètre un nœud root et une valeur, et insère cette valeur dans l'arbre binaire de recherche correspondant. Assurez-vous que les valeurs plus petites sont insérées à gauche et les valeurs plus grandes à droite.
def insert(root, value):
if root is None:
return Node(value)
if value < root.value:
root.left = insert(root.left, value)
else:
root.right = insert(root.right, value)
return rootImplémentez une fonction récursive preorder_traversal qui prend en paramètre un nœud root et effectue un parcours préfixe (préordre) de l'arbre en imprimant les valeurs des nœuds.
def preorder_traversal(root):
if root is not None:
print(root.value, end=" ")
preorder_traversal(root.left)
preorder_traversal(root.right)Implémentez une fonction récursive search qui prend en paramètre un nœud root et une valeur, et recherche cette valeur dans l'arbre binaire. La fonction doit renvoyer True si la valeur est présente et False sinon.
def search(root, value):
if root is None or root.value == value:
return root is not None
if value < root.value:
return search(root.left, value)
else:
return search(root.right, value)Les mathématiques ont souvent la réputation d'être une discipline austère et difficile, mais ...
Read more.Plongez dans l'univers fascinant des suites numériques, où chaque terme révèle des patterns surprenants et des applications pratiques dans les mathématiques et au-delà.
Read more.Découvrez comment les fonctions tissent des liens entre les nombres et les concepts, transformant des idées abstraites en outils puissants pour résoudre des problèmes du quotidien.
Read more.Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !