1. Introduction à la méthode Diviser pour Régner :

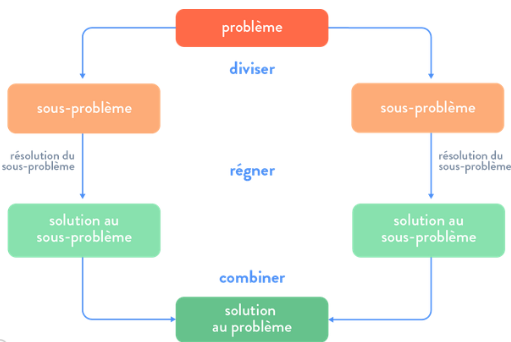
• La méthode Diviser pour Régner est une technique de conception algorithmique qui consiste à diviser un problème en sous-problèmes plus petits, les résoudre de manière récursive, puis combiner les solutions pour obtenir la solution finale.
• Cette approche est basée sur la récursion et est souvent utilisée pour résoudre des problèmes complexes en les décomposant en problèmes plus simples.

2. Étapes de la méthode Diviser pour Régner:

• Diviser : Divisez le problème initial en sous-problèmes plus petits de taille réduite.
• Régner : Résolvez récursivement chaque sous-problème de manière indépendante.
• Combiner : Combinez les solutions des sous-problèmes pour obtenir la solution finale au problème initial.

3. Exemple classique : Tri fusion (Merge Sort) :

• Le tri fusion est un exemple courant d'algorithme basé sur la méthode Diviser pour Régner.
• Voici les étapes de l'algorithme de tri fusion :
  •         1️⃣ Diviser : Divisez la liste non triée en deux moitiés égales.
  •         2️⃣ Régner : Récursivement, triez chaque moitié de la liste.
  •         3️⃣ Combiner : Fusionnez les deux moitiés triées pour obtenir la liste triée finale.

4. Exemple de code Python pour le tri fusion :

def fusionner(liste, gauche, milieu, droite):
    n1 = milieu - gauche + 1
    n2 = droite - milieu

    # Créer des listes temporaires pour stocker les sous-listes gauche et droite
    gauche_temp = [0] * n1
    droite_temp = [0] * n2

    # Copier les données dans les listes temporaires
    for i in range(n1):
        gauche_temp[i] = liste[gauche + i]
    for j in range(n2):
        droite_temp[j] = liste[milieu + 1 + j]

    # Fusionner les sous-listes gauche et droite
    i = 0  # indice initial de la première sous-liste
    j = 0  # indice initial de la deuxième sous-liste
    k = gauche  # indice initial de la liste fusionnée

    while i < n1 and j < n2:
        if gauche_temp[i] <= droite_temp[j]:
            liste[k] = gauche_temp[i]
            i += 1
        else:
            liste[k] = droite_temp[j]
            j += 1
        k += 1

    # Copier les éléments restants de la sous-liste gauche
    while i < n1:
        liste[k] = gauche_temp[i]
        i += 1
        k += 1

    # Copier les éléments restants de la sous-liste droite
    while j < n2:
        liste[k] = droite_temp[j]
        j += 1
        k += 1

def tri_fusion(liste):
    if len(liste) > 1:
        milieu = len(liste) // 2
        gauche = liste[:milieu]
        droite = liste[milieu:]

        tri_fusion(gauche)  # Tri de la sous-liste gauche
        tri_fusion(droite)  # Tri de la sous-liste droite

        fusionner(liste, 0, milieu - 1, len(liste) - 1)  # Fusion des deux sous-listes triées

# Exemple d'utilisation du tri fusion
liste = [64, 34, 25, 12, 22, 11, 90]
tri_fusion(liste)
print(liste)  # Affiche [11, 12, 22, 25, 34, 64, 90]

3. Conclusion

La méthode Diviser pour Régner est une approche puissante pour résoudre des problèmes complexes en les décomposant en sous-problèmes plus simples, les résolvant de manière récursive, puis en combinant les solutions pour obtenir la solution finale. Cette méthode repose sur la récursion et permet de résoudre efficacement de nombreux problèmes algorithmiques.

Exercice 1: ★ ★ ★ ★ ☆

Écrire une fonction récursive pour calculer la somme des éléments d'une liste en utilisant la méthode Diviser pour Régner.
1. Écrire une fonction somme_liste(liste) qui retourne la somme des éléments de la liste.
2. Tester votre fonction avec la liste [1, 2, 3, 4, 5].

Exercice 2: ★ ★ ★ ★ ★

Créer un algorithme de recherche binaire en utilisant la méthode Diviser pour Régner.
1. Écrire une fonction recherche_binaire(liste, valeur) qui retourne l'index de valeur dans liste triée, ou -1 si la valeur n'est pas présente.
2. Tester votre fonction avec une liste triée et une valeur à rechercher.

Exercice 3: ★ ★ ★ ★ ☆

Écrire une fonction pour trouver le maximum d'une liste en utilisant la méthode Diviser pour Régner.
1. Écrire une fonction maximum_liste(liste) qui retourne le plus grand élément de la liste.
2. Tester votre fonction avec la liste [7, 2, 9, 4, 5].

Exercice 4: ★ ★ ★ ★ ★

Créer un algorithme pour calculer le produit des éléments d'une liste en utilisant la méthode Diviser pour Régner.
1. Écrire une fonction produit_liste(liste) qui retourne le produit des éléments de la liste.
2. Tester votre fonction avec la liste [2, 3, 4].

Exercice 5: ★ ★ ★ ★ ☆

Écrire une fonction pour trier une liste en utilisant la méthode Diviser pour Régner (Tri fusion).
1. Écrire une fonction tri_fusion(liste) qui trie les éléments de la liste en utilisant l'algorithme de tri fusion.
2. Tester votre fonction avec la liste [38, 27, 43, 3, 9, 82, 10].