Exercices corrigés sur les réseaux
Considérez le réseau suivant composé des routeurs A, B, C, et D, connectés entre eux :
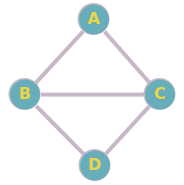
Créez la table de routage pour chaque routeur en utilisant le protocole RIP.
Pour créer la table de routage pour chaque routeur (A, B, C, D) en utilisant le protocole RIP,
nous allons établir les routes en fonction des informations fournies dans le réseau.
Le protocole RIP utilise un chemin de coût basé sur le nombre de sauts. Voici comment les tables de routage peuvent être établies :
Table de routage pour le routeur A
Destination
Next Hop
Coût
B
B
1
C
C
1
D
B
2
Table de routage pour le routeur B
Destination
Next Hop
Coût
A
A
1
C
C
1
D
D
1
Table de routage pour le routeur C
Destination
Next Hop
Coût
A
A
1
B
B
1
D
B
2
Table de routage pour le routeur D
Destination
Next Hop
Coût
B
B
1
C
C
1
A
B
2
Explication des tables
• Routeur A :
• Peut atteindre B et C directement avec un coût de 1.
• Pour atteindre D, il passe par B, donc le coût est de 2.
• Routeur B :
Peut atteindre A, C, et D directement avec un coût de 1.
• Routeur C :
• Peut atteindre A et B directement avec un coût de 1.
• Pour atteindre D, il passe par B, donc le coût est de 2.
• Routeur D :
• Peut atteindre B et C directement avec un coût de 1.
• Pour atteindre A, il passe par B, donc le coût est de 2.
Ces tables de routage représentent les chemins optimaux selon le protocole RIP pour le réseau donné.
Cet exercice porte sur les réseaux en général et les protocoles RIP et OSPF en particulier.
On considère un réseau composé de plusieurs routeurs reliés de la façon suivante :
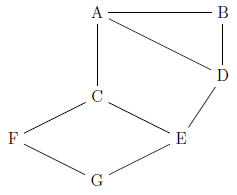
Le protocole RIP
Le protocole RIP permet de construire les tables de routage des différents routeurs, en indiquant pour chaque routeur la distance, en nombre de sauts, qui le sépare d’un autre routeur. Pour le réseau ci-dessus, on dispose des tables de routage suivantes :
Table de routage pour le routeur A
| Destination | Routeur suivant | Distance |
|---|---|---|
| B | B | 1 |
| C | C | 1 |
| D | D | 1 |
| E | C | 2 |
| F | C | 2 |
| G | C | 3 |
| Destination | Routeur suivant | Distance |
|---|---|---|
| A | A | 1 |
| C | A | 2 |
| D | D | 1 |
| E | D | 2 |
| F | A | 3 |
| G | D | 3 |
| Destination | Routeur suivant | Distance |
|---|---|---|
| A | A | 1 |
| B | A | 2 |
| D | E | 2 |
| E | E | 1 |
| F | F | 1 |
| G | F | 2 |
| Destination | Routeur suivant | Distance |
|---|---|---|
| A | A | 1 |
| B | B | 1 |
| C | E | 2 |
| E | E | 1 |
| F | A | 3 |
| G | E | 2 |
| Destination | Routeur suivant | Distance |
|---|---|---|
| A | C | 2 |
| B | D | 2 |
| C | C | 1 |
| D | D | 1 |
| F | G | 2 |
| G | G | 1 |
| Destination | Routeur suivant | Distance |
|---|---|---|
| A | C | 2 |
| B | C | 3 |
| C | C | 1 |
| D | C | 3 |
| E | G | 2 |
| G | G | 1 |

| Destination | Routeur suivant | Distance |
|---|---|---|
| A | E | 2 |
| B | D | 2 |
| C | F | 1 |
| D | E | 1 |
| F | G | 1 |
| G | G | 1 |
| Destination | Routeur suivant | Distance |
|---|---|---|
| A | A | 0 |
| B | B | 1 |
| D | D | 1 |
| E | B | 2 |
| F | D | 3 |
| G | D | 4 |
Cet exercice porte sur les représentations binaires et les protocoles de routage.
1. Une adresse IPv4 est représentée sous la forme de 4 nombres séparés par des points. Chacun de ces 4 nombres peut être représenté sur un octet.
a. Donner en écriture décimale l’adresse IPv4 correspondant à l’écriture binaire :
11000000.10101000.10000000.10000011
b. Tous les ordinateurs du réseau A ont une adresse IPv4 de la forme :
192.168.128._ _ _ , où seul le dernier octet (représenté par _ _ _ ) diffère.
Donner le nombre d’adresses différentes possibles du réseau A.
2. On rappelle que le protocole RIP cherche à minimiser le nombre de routeurs traversés (qui correspond à la métrique). On donne les tables de routage d’un réseau informatique composé de 5 routeurs (appelés A, B, C, D et E), chacun associé directement à un réseau du même nom obtenues avec le protocole RIP :
Routeur A
| Destination | Métrique |
|---|---|
| A | 0 |
| B | 1 |
| C | 1 |
| D | 1 |
| E | 2 |
| Destination | Métrique |
|---|---|
| A | 1 |
| B | 0 |
| C | 2 |
| D | 1 |
| E | 2 |
| Destination | Métrique |
|---|---|
| A | 1 |
| B | 2 |
| C | 0 |
| D | 1 |
| E | 2 |
| Destination | Métrique |
|---|---|
| A | 1 |
| B | 1 |
| C | 1 |
| D | 0 |
| E | 1 |
| Destination | Métrique |
|---|---|
| A | 2 |
| B | 2 |
| C | 2 |
| D | 1 |
| E | 0 |
a. Donner la liste des routeurs avec lesquels le routeur A est directement relié.
b. Représenter(en json) et de manière sommaire les 5 routeurs ainsi que les liaisons existantes entre ceux-ci.
3. Le protocole OSPF est un protocole de routage qui cherche à minimiser la somme des métriques des liaisons entre routeurs.
Dans le protocole de routage OSPF le débit des liaisons entre routeurs agit sur la métrique via la relation :
\(metrique = \frac{10^8}{debit}\)
dans laquelle le débit est exprimé en bit par seconde (bps).
On rappelle qu’un kbps est égal à \(10^3\) bps et qu’un Mbps est égal à \(10^6\) bps.
Recopier sur votre copie et compléter le tableau suivant :
| Débit | 100 kbps | 500 kbps | ? | 100 Mbps |
|---|---|---|---|---|
| Métrique associée | 1000 | ? | 10 | 1 |
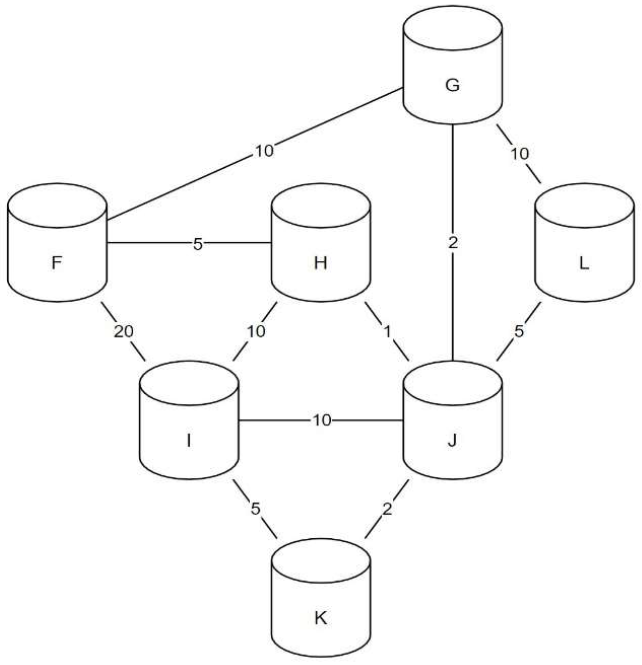
| Destination | Métrique |
|---|---|
| F | 0 |
| G | 8 |
| H | 5 |
| I | |
| J | |
| K | |
| L |
Les nombres présents sur les liaisons représentent les coûts des routes avec le protocole OSPF.
a. Indiquer le chemin emprunté par un message d’un ordinateur du réseau F à destination d’un ordinateur du réseau I.
Justifier votre réponse.
b. Recopier et compléter la table de routage du routeur F.
c. Citer une unique panne qui suffirait à ce que toutes les données des échanges de tout autre réseau à destination du réseau F transitent par le routeur G.
Expliquer en détail votre réponse.

| Débit | 100 kbps | 500 kbps | 1 Mbps | 100 Mbps |
|---|---|---|---|---|
| Métrique associée | 1000 | 200 | 100 | 1 |
| Destination | Métrique |
|---|---|
| F | 0 |
| G | 8 |
| H | 5 |
| I | 15 |
| J | 10 |
| K | 25 |
| L | 20 |
Cet exercice porte sur les réseaux et les protocoles de routage.
On représente ci-dessous un réseau dans lequel R1, R2, R3, R4, R5 et R6 sont des routeurs.
Le réseau local L1 est relié au routeur R1 et le réseau local L2 au routeur R6.
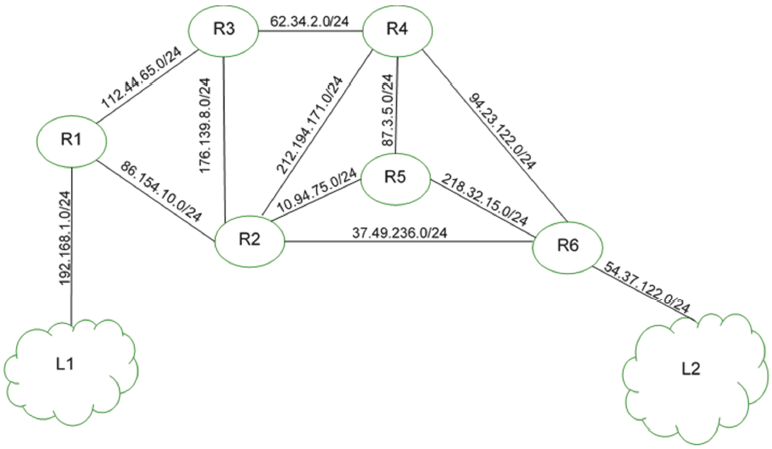
Rappels et notations
Dans cet exercice, les adresses IP sont composées de 4 octets, soit 32 bits. Elles sont notées X1.X2.X3.X4, où X1, X2, X3 et X4 sont les valeurs des 4 octets, convertis en notation décimale.
La notation X1.X2.X3.X4/n signifie que les n premiers bits de poids forts de l’adresse IP représentent la partie « réseau », les bits suivants représentent la partie « hôte ».
Toutes les adresses des hôtes connectés à un réseau local ont la même partie réseau et peuvent donc communiquer directement. L’adresse IP dont tous les bits de la partie « hôte » sont à 0 est appelée « adresse du réseau ».
On donne également des extraits de la table de routage des routeurs R1 à R5 dans le
tableau suivant :
| Routeur | Réseau destinataire | Passerelle | Interface |
|---|---|---|---|
| R1 | 54.37.122.0/24 | 86.154.10.1 | 86.154.10.56 |
| R2 | 54.37.122.0/24 | 37.49.236.22 | 37.49.236.23 |
| R3 | 54.37.122.0/24 | 62.34.2.8 | 62.34.2.9 |
| R4 | 54.37.122.0/24 | 94.23.122.10 | 94.23.122.11 |
| R5 | 54.37.122.0/24 | 218.32.15.1 | 218.32.15.2 |
1. Un paquet part du réseau local L1 à destination du réseau local L2.
a. En utilisant l’extrait de la table de routage de R1, vers quel routeur R1 envoie t- il ce paquet : R2 ou R3 ? Justifier.
b. A l’aide des extraits de tables de routage ci-dessus, nommer les routeurs traversés par ce paquet, lorsqu’il va du réseau L1 au réseau L2.
2. La liaison entre R1 et R2 est rompue.
a. Sachant que ce réseau utilise le protocole RIP (distance en nombre de sauts), donner l’un des deux chemins possibles que pourra suivre un paquet allant de L1 vers L2.
b. Dans les extraits de tables de routage ci-dessus, pour le chemin de la question 2.a, quelle(s) ligne(s) sera (seront) modifiée(s) ?
3. On a rétabli la liaison entre R1 et R2.
Par ailleurs, pour tenir compte du débit des liaisons, on décide d’utiliser le protocole OSPF (distance liée au coût minimal des liaisons) pour effectuer le routage. Le coût des liaisons entre les routeurs est donné par le tableau suivant :
| Liaison | R1-R2 | R1-R3 | R2-R3 | R2-R4 | R2-R5 | R2-R6 | R3-R4 | R4-R5 | R4-R6 | R5-R6 |
|---|---|---|---|---|---|---|---|---|---|---|
| Coût | 100 | 100 | ? | 1 | 10 | 10 | 10 | 1 | 10 | 1 |
a. Le coût \(C\) d’une liaison est donné ici par la formule
\(C = \frac{10^9}{BP}\)
où \({BP}\) est la bande passante de la connexion en bps (bit par seconde).
Sachant que la bande passante de la liaison R2-R3 est de 10 Mbps, calculer le coût correspondant.
b. Déterminer le chemin parcouru par un paquet partant du réseau L1 et arrivant au réseau L2, en utilisant le protocole OSPF.
c. Indiquer pour quel(s) routeur(s) l’extrait de la table de routage sera modifié
pour un paquet à destination de L2, avec la métrique OSPF.
Les mathématiques ont souvent la réputation d'être une discipline austère et difficile, mais ...
Read more.Plongez dans l'univers fascinant des suites numériques, où chaque terme révèle des patterns surprenants et des applications pratiques dans les mathématiques et au-delà.
Read more.Découvrez comment les fonctions tissent des liens entre les nombres et les concepts, transformant des idées abstraites en outils puissants pour résoudre des problèmes du quotidien.
Read more.Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !