Exercices corrigés sur les structures des données
Considérons le mot "informatique". Nous allons construire une pile en empilant successivement toutes les lettres du mot, en commençant par la première lettre \(I\) et en terminant par la dernière lettre \(E\).
• Première étape : Dépiler une lettre.
Quelle est la lettre qui se trouve au sommet de la pile et qui sera dépilée en premier ?
• Deuxième étape : Dépiler cinq lettres.
Après avoir dépilé cinq lettres supplémentaires, quelle lettre se trouve maintenant au sommet de la pile ?
Pour résoudre ce problème, nous allons examiner les étapes de l'empilage et du dépilage de lettres du mot "informatique".
1. Empilage des lettres du mot "informatique" :
Le mot "informatique" est empilé lettre par lettre, en commençant par la première lettre 'i' et en terminant par la dernière lettre 'e'. Voici l'ordre des lettres empilées :
Empilage : i, n, f, o, r, m, a, t, i, q, u, e
La pile ressemble à ceci, avec 'e' en haut :
Sommet → e
u
q
i
t
a
m
r
o
f
n
Bas → i
2. Première étape : Dépiler une lettre :
La lettre qui se trouve au sommet de la pile et qui sera dépilée en premier est 'e'.
Après avoir dépilé 'e', la pile ressemble à ceci :
Sommet → u
q
i
t
a
m
r
o
f
n
Bas → i
3. Deuxième étape : Dépiler cinq lettres supplémentaires :
Nous dépilons maintenant cinq lettres supplémentaires, ce qui signifie dépiler successivement les lettres u, q, i, t, a.
Après avoir dépilé ces cinq lettres, la pile ressemble à ceci :
Sommet → m
r
o
f
n
Bas → i
La lettre qui se trouve maintenant au sommet de la pile est 'm'.
Résumé :
• La lettre dépilée en premier est 'e'.
• Après avoir dépilé cinq lettres supplémentaires, la lettre au sommet de la pile est 'm'.
On forme une file en empilant successivement toutes les lettres du mot informatique en commençant donc par le \(I\).
1. On défile une lettre. Quelle est cette lettre ?
2. On défile maintenant 5 lettres. Quel élément se trouve alors au sommet de la file ?
Pour résoudre ce problème, nous devons examiner les étapes de l'empilage et du défilement des lettres du mot "informatique" en utilisant une file. Une file (ou queue) suit la règle FIFO (First In, First Out), c'est-à-dire que les éléments sont défilés dans l'ordre dans lequel ils ont été empilés.
1. Empilage des lettres du mot "informatique" :
Le mot "informatique" est empilé lettre par lettre, en commençant par la première lettre 'i' et en terminant par la dernière lettre 'e'. Voici l'ordre des lettres empilées dans la file :
Empilage : i, n, f, o, r, m, a, t, i, q, u, e
La file ressemble à ceci, avec 'i' en tête (début) :
Tête → i
n
f
o
r
m
a
t
i
q
u
Fin → e
2. Première étape : Défiler une lettre :
La lettre qui se trouve à la tête de la file et qui sera défilée en premier est 'i'.
Après avoir défilé 'i', la file ressemble à ceci :
Tête → n
f
o
r
m
a
t
i
q
u
Fin → e
3. Deuxième étape : Défiler cinq lettres supplémentaires :
Nous défilons maintenant cinq lettres supplémentaires, ce qui signifie défiler successivement les lettres n, f, o, r, m.
Après avoir défilé ces cinq lettres, la file ressemble à ceci :
Tête → a
t
i
q
u
Fin → e
La lettre qui se trouve maintenant à la tête de la file est 'a'.
Résumé :
• La lettre défilée en premier est 'i'.
• Après avoir défilé cinq lettres supplémentaires, la lettre à la tête de la file est 'a'.
Nous disposons de trois piles : \(P_1\), \(P_2\), et \(P_3\).
• \(P_1\) contient des nombres entiers positifs empilés, par exemple : 4 9 2 5 3 8 (où 8 est au sommet de la pile).
• Les piles \(P_2\) et \(P_3\) sont initialement vides.
Manipulez les piles en utilisant des opérations de dépilage et d'empilage pour résoudre les problèmes suivants. Pour chaque problème, décrivez les manipulations nécessaires, rédigez l'algorithme en pseudo-code, puis implémentez-le en Python.
1. Inversion de la Pile \(P_1\) : Inversez l'ordre des éléments dans la pile \(P_1\).
• Description des manipulations : Quelle série de dépilements et d'empilements devez-vous effectuer pour obtenir l'ordre inverse des éléments dans \(P_1\) ?
• Pseudo-code : Écrivez un algorithme en pseudo-code pour inverser l'ordre des éléments de P1.
• Implémentation en Python : Codez l'algorithme en Python.
2. Déplacement Alterné : Déplacez un entier sur deux de la pile \(P_1\) vers les piles \(P_2\) ou \(P_3\).
• Description des manipulations : Comment allez-vous déplacer un entier sur deux vers \(P_2\) ou \(P_3\) ?
• Pseudo-code : Écrivez un algorithme en pseudo-code pour réaliser ce déplacement alterné.
• Implémentation en Python : Codez l'algorithme en Python.
3. Séparation Pair / Impair : Déplacez les entiers de \(P_1\) de manière à ce que les entiers pairs soient dans \(P_2\) et les entiers impairs soient dans \(P_3\).
• Description des manipulations : Quelle série de dépilements et d'empilements devez-vous effectuer pour séparer les entiers pairs et impairs dans \(P_2\) et \(P_3\) respectivement ?
• Pseudo-code : Écrivez un algorithme en pseudo-code pour séparer les entiers pairs et impairs.
• Implémentation en Python : Codez l'algorithme en Python.
1. Inversion de la Pile P1 :
Description des manipulations :
Pour inverser l'ordre des éléments dans la pile P1, nous allons utiliser les piles P2 et P3 de la manière suivante :
1. Dépiler un élément de P1 et l'empiler dans P2.
2. Répéter l'étape 1 jusqu'à ce que P1 soit vide.
3. Dépiler un élément de P2 et l'empiler dans P1.
4. Répéter l'étape 3 jusqu'à ce que P2 soit vide.
Pseudo-code :Implémentation en Python :function inverser_pile(P1, P2, P3): while not est_vide(P1): x = depiler(P1) empiler(P2, x) while not est_vide(P2): x = depiler(P2) empiler(P1, x)2. Déplacement Alterné :def inverser_pile(P1, P2, P3): while P1: x = P1.pop() P2.append(x) while P2: x = P2.pop() P1.append(x)
Description des manipulations :
Pour déplacer un entier sur deux de P1 vers P2 ou P3, nous allons procéder ainsi :
1. Dépiler un élément de P1 et l'empiler dans P2.
2. Dépiler un élément de P1 et l'ignorer (ne pas l'empiler).
3. Répéter les étapes 1 et 2 jusqu'à ce que P1 soit vide.
Pseudo-code :Implémentation en Python :function deplacement_alterne(P1, P2, P3): while not est_vide(P1): x = depiler(P1) empiler(P2, x) if not est_vide(P1): depiler(P1)3. Séparation Pair / Impair :def deplacement_alterne(P1, P2, P3): while P1: x = P1.pop() P2.append(x) if P1: P1.pop()
Description des manipulations :
Pour séparer les entiers pairs et impairs dans P2 et P3 respectivement, nous allons procéder ainsi :
1. Dépiler un élément de P1.
2. Si l'élément est pair, l'empiler dans P2. Sinon, l'empiler dans P3.
3. Répéter les étapes 1 et 2 jusqu'à ce que P1 soit vide.
Pseudo-code :Implémentation en Python :function separation_pair_impair(P1, P2, P3): while not est_vide(P1): x = depiler(P1) if x % 2 == 0: empiler(P2, x) else: empiler(P3, x)Les implémentations Python utilisent des listes Python pour représenter les piles, avec les méthodes `pop()` et `append()` pour simuler les opérations d'empilage et de dépilage.def separation_pair_impair(P1, P2, P3): while P1: x = P1.pop() if x % 2 == 0: P2.append(x) else: P3.append(x)
Nous disposons de deux piles : \(P_1\) et \(P_2\). L'objectif est de créer une structure de donnée de type File en utilisant ces deux piles.
• \(P_1\) contiendra les valeurs de la file. Le sommet de \(P_1\) représentera la tête de la file.
• \(P_2\) est une pile auxiliaire que nous utiliserons pour les manipulations.
Répondez aux questions suivantes en utilisant uniquement les opérations de piles (empiler et dépiler) pour simuler les opérations de la file. Décrivez les manipulations nécessaires, écrivez l'algorithme en pseudo-code, puis implémentez-le en Python.
1. Vérification de la File Vide : Comment vérifier si la file est vide ?
• Description des manipulations : Quelle série d'opérations devez-vous effectuer pour vérifier si la file est vide ?
• Pseudo-code : Écrivez un algorithme en pseudo-code pour vérifier si la file est vide.
• Implémentation en Python : Codez l'algorithme en Python.
2. Défilement de l'Élément de Tête : Comment défiler l'élément en tête de la file ?
• Description des manipulations : Quelle série de dépilements et d'empilements dans les piles P1 et P2 permet de retirer l'élément de tête de la file ?
• Pseudo-code : Écrivez un algorithme en pseudo-code pour défiler l'élément de tête de la file.
• Implémentation en Python : Codez l'algorithme en Python.
3. Enfilage d'un Élément : Comment enfiler un élément à la fin de la file (c'est-à-dire en queue de \(P_1\)) ?
• Description des manipulations : Quelle série de dépilements et d'empilements devez-vous effectuer pour ajouter un élément en fin de file ?
• Pseudo-code : Écrivez un algorithme en pseudo-code pour enfiler un élément en fin de file.
• Implémentation en Python : Codez l'algorithme en Python.
solution en cours
Soit une pile \(P\) composée des éléments suivants : 12, 14, 8, 7, 19 et 22 (le sommet de la pile est 22) .
1. Que renvoie \(depiler(P)\) ? De quels éléments est maintenant composée \(P\) ?
2. On effectue \(empiler(P,42)\). De quels éléments est maintenant composée \(P\) ?
3. Que renvoie \(sommet(P)\) ? La pile est elle modifiée ?
4. Après avoir appliqué \(depiler(P)\) une fois, Quelle est la taille de la pile ?
5. Si on applique \(depiler(P)\) 6 fois de suite, que renvoie \(est\_vide(P)\) ?
1. Que renvoie `depiler(P)` ? De quels éléments est maintenant composée `P` ?
• `depiler(P)` renvoie l'élément se trouvant au sommet de la pile, soit `22`.
• Après l'opération, la pile `P` est composée des éléments suivants : `12, 14, 8, 7, 19`.
2. On effectue `empiler(P,42)`. De quels éléments est maintenant composée `P` ?
Après avoir empilé l'élément `42` sur la pile `P`, celle-ci est maintenant composée des éléments suivants : `12, 14, 8, 7, 19, 42`.
3. Que renvoie `sommet(P)` ? La pile est-elle modifiée ?
• `sommet(P)` renvoie l'élément se trouvant au sommet de la pile, soit `42`.
• La pile `P` n'est pas modifiée par l'opération `sommet(P)`.
4. Après avoir appliqué `depiler(P)` une fois, quelle est la taille de la pile ?
• Après avoir dépilé une fois, la pile `P` est composée des éléments suivants : `12, 14, 8, 7, 19`.
• La taille de la pile est maintenant de 5 éléments.
5. Si on applique `depiler(P)` 6 fois de suite, que renvoie `est_vide(P)` ?
• Après avoir dépilé 6 fois, la pile `P` est maintenant vide.
• `est_vide(P)` renvoie `True`, indiquant que la pile est vide.
Soit une file \(F\) composée des éléments suivants : 12, 14, 8, 7, 19 et 22 (le premier élément rentré dans la file est 22 ; le dernier élément rentré dans la file est 12).
1. On effectue \(enfiler(F,42)\). De quels éléments est maintenant composée F ?
2. Que renvoie \(defiler(F)\) ? De quels éléments est maintenant composée F ?
3. Que renvoie \(tete(F)\) ? La file est elle modifiée?
4. si on applique \(defiler(F)\) 6 fois de suite, que renvoie \(est\_vide(F)\) ?
1. On effectue `enfiler(F,42)`. De quels éléments est maintenant composée `F` ?
Après avoir enfilé l'élément `42` dans la file `F`, celle-ci est maintenant composée des éléments suivants : `22, 12, 14, 8, 7, 19, 42`.
2. Que renvoie `defiler(F)` ? De quels éléments est maintenant composée `F` ?
• `defiler(F)` renvoie le premier élément de la file, soit `22`.
• Après l'opération, la file `F` est composée des éléments suivants : `12, 14, 8, 7, 19, 42`.
3. Que renvoie `tete(F)` ? La file est-elle modifiée ?
• `tete(F)` renvoie le premier élément de la file, soit `12`.
• La file `F` n'est pas modifiée par l'opération `tete(F)`.
4. Si on applique `defiler(F)` 6 fois de suite, que renvoie `est_vide(F)` ?
• Après avoir défilé 6 fois, la file `F` est maintenant vide.
• `est_vide(F)` renvoie `True`, indiquant que la file est vide.
Ecrire un algorithme (en python) pour chacun des problèmes suivants. En faire la preuve et déterminer la complexité.
• Supprimer tous les éléments d'une file situés au dessus d'un valeur donnée.
• Transférer le contenu d'une file vers une autre file.
• Vérifier si une valeur donnée appartient à une file.
• Calculer la taille d'une file.
• Ne conserver qu'une seule occurrence d'une valeur donnée dans une file.
• Purger une file : supprimer toutes les occurrences multiples d'une file (càd ne garder qu'un exemplaire de chaque valeur de la file).
1. Liste chaînée (Linked List) : Une liste chaînée est une structure de données linéaire où chaque élément contient une référence au suivant. Cela permet d'insérer et de supprimer des éléments en temps constant, ce qui en fait une bonne alternative à la deque.2. Liste doublement chaînée (Doubly Linked List) : Une liste doublement chaînée est similaire à la liste chaînée, mais chaque nœud contient une référence au nœud précédent et au nœud suivant. Cela permet d'accéder plus facilement aux éléments dans les deux directions.class Node: def __init__(self, data): self.data = data self.next = None class LinkedList: def __init__(self): self.head = None def append(self, data): new_node = Node(data) if self.head is None: self.head = new_node return last_node = self.head while last_node.next: last_node = last_node.next last_node.next = new_node def insert_at_beginning(self, data): new_node = Node(data) new_node.next = self.head self.head = new_node3. Liste circulaire (Circular List) : Une liste circulaire est une variante de la liste chaînée où le dernier nœud pointe vers le premier nœud, formant une boucle.class Node: def __init__(self, data): self.data = data self.prev = None self.next = None class DoublyLinkedList: def __init__(self): self.head = None def append(self, data): new_node = Node(data) if self.head is None: self.head = new_node return last_node = self.head while last_node.next: last_node = last_node.next last_node.next = new_node new_node.prev = last_node def insert_at_beginning(self, data): new_node = Node(data) new_node.next = self.head if self.head is not None: self.head.prev = new_node self.head = new_nodeclass Node: def __init__(self, data): self.data = data self.next = None class CircularLinkedList: def __init__(self): self.head = None def append(self, data): new_node = Node(data) if self.head is None: self.head = new_node new_node.next = self.head return last_node = self.head while last_node.next != self.head: last_node = last_node.next last_node.next = new_node new_node.next = self.head def insert_at_beginning(self, data): new_node = Node(data) if self.head is None: self.head = new_node new_node.next = self.head return last_node = self.head while last_node.next != self.head: last_node = last_node.next new_node.next = self.head self.head = new_node last_node.next = self.head
Ecrire un algorithme qui :
• Transfert le contenu d'une file dans une pile.
• Ecrire un algorithme qui transfert le contenu d'une pile dans une file.
• Ecrire un algorithme qui inverse une pile.
• Ecrire un algorithme qui inverse une file.
• Ecrire un algorithme qui fusionne deux piles.
• Ecrire un algorithme qui fusionne deux files.
1. Transfert du contenu d'une file dans une pile:2. Transfert du contenu d'une pile dans une file:def transfer_queue_to_stack(queue, stack): while queue: stack.append(queue.pop(0))3. Inversion d'une pile:def transfer_stack_to_queue(stack, queue): while stack: queue.append(stack.pop())4. Inversion d'une file:def reverse_stack(stack): temp_stack = [] while stack: temp_stack.append(stack.pop()) return temp_stack5. Fusion de deux piles:def reverse_queue(queue): stack = [] while queue: stack.append(queue.pop(0)) return stack6. Fusion de deux files:def merge_stacks(stack1, stack2): merged_stack = [] while stack1 or stack2: if stack1: merged_stack.append(stack1.pop()) if stack2: merged_stack.append(stack2.pop()) return merged_stackdef merge_queues(queue1, queue2): merged_queue = [] while queue1 or queue2: if queue1: merged_queue.append(queue1.pop(0)) if queue2: merged_queue.append(queue2.pop(0)) return merged_queue
On dispose d'une file \(F_1\) qui contient les éléments suivants classés par ordre alphabétique :
\[F_1=('A','B','C','D','E')\]
1. Quel est l'élément issu du défilage de \(F_1\) ?
2. Proposer un algorithme écrit en1. Parcours en profondeur (DFS) :
Pour le graphe non orienté suivant, effectuez un parcours en profondeur (DFS) en partant du sommet A. Listez les sommets dans l'ordre de leur visite.
Sommets : A, B, C, D, E
Arêtes : (A-B), (A-C), (B-D), (C-E), (D-E)
2. Parcours en largeur (BFS) :
Pour le même graphe que ci-dessus, effectuez un parcours en largeur (BFS) en partant du sommet A. Listez les sommets dans l'ordre de leur visite. python qui utilise deux piles \(P_1\) et \(P_2\) et qui permet la saisie d'affilée des 5 éléments (sans sortie intermédiaire) et la sortie des éléments comme s'ils sortaient d'une file.
1. L'élément issu du défilage de F1 :
Étant donné que nous utilisons une file (queue) qui suit la règle FIFO (First In, First Out), l'élément qui sera défilé en premier de F1 est le premier élément ajouté à la file. Comme les éléments sont classés par ordre alphabétique et la file est :
F1 = ('A', 'B', 'C', 'D', 'E')
L'élément défilé en premier est 'A'.
2. Pour défilage, nous devons transférer tous les éléments de P1 à P2 (ce qui inversera l'ordre), puis dépiler de P2.
Voici un algorithme Python pour ce processus :Explication du code :class FileAvecDeuxPiles: def __init__(self): self.P1 = [] # Pile d'entrée self.P2 = [] # Pile de sortie def enfiler(self, element): # Empiler l'élément dans P1 self.P1.append(element) def defiler(self): # Si P2 est vide, transférer tous les éléments de P1 à P2 if not self.P2: while self.P1: self.P2.append(self.P1.pop()) # Dépiler et retourner l'élément de P2 if self.P2: return self.P2.pop() else: return None # Si les deux piles sont vides # Exemple d'utilisation file = FileAvecDeuxPiles() elements = ['A', 'B', 'C', 'D', 'E'] # Enfiler les éléments for elem in elements: file.enfiler(elem) # Dépiler les éléments comme s'ils sortaient d'une file while True: elem = file.defiler() if elem is None: break print(elem)
1. Classe FileAvecDeuxPiles :
• __init__ : Initialise deux piles, P1 pour l'entrée et P2 pour la sortie.
• enfiler : Empile un élément dans P1.
• defiler : Si P2 est vide, transfère tous les éléments de P1 à P2 (cela inverse l'ordre des éléments), puis dépile et retourne l'élément de P2.
2. Utilisation :
• Nous créons une instance de FileAvecDeuxPiles.
• Nous ajoutons les éléments ['A', 'B', 'C', 'D', 'E'] à la file.
• Nous dépilons et affichons les éléments jusqu'à ce que la file soit vide.
Ce code affiche les éléments dans l'ordre 'A', 'B', 'C', 'D', 'E', imitant le comportement d'une file.
Simuler en python une structure de données de type File en utilisant uniquement deux piles, \(P_1\) et \(P_2\). Pour ce faire, \(P_1\) sera utilisée pour enfiler les éléments dans la file et \(P_2\) sera utilisée pour défiler les éléments de la file.
class FileAvecDeuxPiles:
def __init__(self):
self.P1 = [] # Pile pour enfiler
self.P2 = [] # Pile pour défiler
def enqueue(self, value):
self.P1.append(value) # Ajouter l'élément à la pile P1
def dequeue(self):
if not self.P2: # Si la pile P2 est vide
while self.P1: # Déplacer tous les éléments de P1 à P2
self.P2.append(self.P1.pop())
if not self.P2: # Si la pile P2 est toujours vide, la file est vide
return "La file est vide."
return self.P2.pop() # Retirer l'élément en tête de la file
def is_empty(self):
return not self.P1 and not self.P2 # La file est vide si P1 et P2 sont vides
# Exemple d'utilisation
file = FileAvecDeuxPiles()
file.enqueue(10)
file.enqueue(20)
file.enqueue(30)
file.enqueue(40)
print(file.dequeue()) # Affiche 10
print(file.dequeue()) # Affiche 20
print(file.is_empty()) # Affiche False
1. Représentation par une matrice d'adjacence :
Considérez le graphe non orienté suivant :
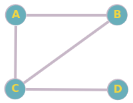
Sommets : A, B, C, D
Arêtes : (A-B), (A-C), (B-C), (C-D)
a. Construisez la matrice d'adjacence du graphe ci-dessus.
b. Quel est le degré de chaque sommet ?
2. Représentation par une liste d'adjacence :
Considérez le graphe orienté suivant :
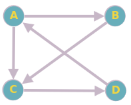
Sommets : A, B, C, D
Arêtes : (A→B), (A→C), (B→C), (C→D), (D→A)
a. Représentez ce graphe par une liste d'adjacence.
b. Quels sont les degrés entrant et sortant de chaque sommet ?
1. Représentation par une matrice d'adjacence
Considérons le graphe non orienté suivant :
Sommets : A, B, C, D
Arêtes : (A-B), (A-C), (B-C), (C-D)
a. Construction de la matrice d'adjacence du graphe ci-dessus:
Une matrice d'adjacence est une matrice carrée utilisée pour représenter un graphe. Si le graphe possède n sommets, la matrice sera de dimension n×n. Les éléments de la matrice sont définis comme suit :
M[i][j] = 1 si le sommet i est adjacent au sommet j.
M[i][j] = 0 sinon.
Pour le graphe donné, les sommets sont A, B, C, et D. La matrice d'adjacence M sera une matrice :
| A | B | C | D | |
|---|---|---|---|---|
| A | 0 | 1 | 1 | 0 |
| B | 1 | 0 | 1 | 0 |
| C | 1 | 1 | 0 | 1 |
| D | 0 | 0 | 1 | 0 |
1. Parcours en profondeur (DFS) :
Pour le graphe non orienté suivant, effectuez un parcours en profondeur (DFS) en partant du sommet A. Listez les sommets dans l'ordre de leur visite.
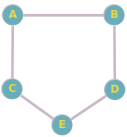
Sommets : A, B, C, D, E
Arêtes : (A-B), (A-C), (B-D), (C-E), (D-E)
2. Parcours en largeur (BFS) :
Pour le même graphe que ci-dessus, effectuez un parcours en largeur (BFS) en partant du sommet A. Listez les sommets dans l'ordre de leur visite.
1. Parcours en profondeur (DFS)
Le parcours en profondeur (DFS) explore aussi loin que possible le long de chaque branche avant de revenir en arrière. Voici le détail de l'exercice :
Graphe donné :
• Sommets : A, B, C, D, E
• Arêtes : (A-B), (A-C), (B-D), (C-E), (D-E)
Étapes du DFS en partant du sommet A :
1. Départ du sommet A. Marquer A comme visité.
• Visité : A
• Pile : [A]
2. Explorer le voisin de A, choisir B (premier voisin non visité). Marquer B comme visité.
• Visité : A, B
• Pile : [A, B]
3. Explorer le voisin de B, choisir D. Marquer D comme visité.
• Visité : A, B, D
• Pile : [A, B, D]
4. Explorer le voisin de D, choisir E (C est non adjacent à D). Marquer E comme visité.
• Visité : A, B, D, E
• Pile : [A, B, D, E]
5. Explorer le voisin de E, revenir en arrière car tous les voisins sont visités ou non accessibles.
6. Retour à D, tous les voisins visités. Revenir à B.
7. Retour à B, explorer C. Marquer C comme visité.
• Visité : A, B, D, E, C
• Pile : [A, B, C]
8. Fin du parcours, tous les sommets sont visités.
Ordre de visite en DFS :
A,B,D,E,C
2. Parcours en largeur (BFS)
Le parcours en largeur (BFS) explore tous les voisins d'un sommet avant de passer aux voisins de ces voisins. Voici le détail de l'exercice :
Graphe donné :
• Sommets : A, B, C, D, E
• Arêtes : (A-B), (A-C), (B-D), (C-E), (D-E)
Étapes du BFS en partant du sommet A :
1. Départ du sommet A. Marquer A comme visité et ajouter à la file d'attente.
• Visité : A
• File d'attente : [A]
2. Défilement de la file, traiter A. Ajouter les voisins non visités B et C à la file.
• Visité : A, B, C
• File d'attente : [B, C]
3. Défilement de la file, traiter B. Ajouter le voisin non visité D à la file.
• Visité : A, B, C, D
• File d'attente : [C, D]
4. Défilement de la file, traiter C. Ajouter le voisin non visité E à la file.
• Visité : A, B, C, D, E
• File d'attente : [D, E]
5. Défilement de la file, traiter D. Tous les voisins sont déjà visités.
• Visité : A, B, C, D, E
• File d'attente : [E]
6. Défilement de la file, traiter E. Tous les voisins sont déjà visités.
• Visité : A, B, C, D, E
• File d'attente : []
7. Fin du parcours, tous les sommets sont visités.
Ordre de visite en BFS :
A,B,C,D,E
Considérez le graphe pondéré suivant :
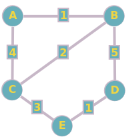
Sommets : A, B, C, D, E
Arêtes pondérées : (A-B, 1), (A-C, 4), (B-C, 2), (B-D, 5), (C-E, 3), (D-E, 1)
Utilisez l'algorithme de Dijkstra pour trouver les plus courts chemins à partir du sommet A vers tous les autres sommets. Listez les distances et les chemins les plus courts.
Algorithme de Dijkstra
L'algorithme de Dijkstra est utilisé pour trouver les plus courts chemins à partir d'un sommet source vers tous les autres sommets dans un graphe pondéré. Voici le détail de l'exercice :
Graphe donné :
• Sommets : A, B, C, D, E
• Arêtes pondérées : (A-B, 1), (A-C, 4), (B-C, 2), (B-D, 5), (C-E, 3), (D-E, 1)
Étapes de l'algorithme de Dijkstra :
1. Initialisation :
• Distance de A à lui-même est 0 : d(A)=0
• Distance de A à tous les autres sommets est infinie : d(B) = ∞, d(C) = ∞, d(D) = ∞, d(E)= ∞
• Prédécesseur de chaque sommet est inconnu : prédécesseur(B) = NIL, prédécesseur(C) = NIL,prédécesseur(D) = NIL,prédécesseur(E) = NIL.
• Ensemble des sommets non traités : Q = {A,B,C,D,E}
2. Choisir le sommet avec la plus petite distance non traitée (initialement A) et le marquer comme traité :
• Sommet courant = A
• Q = {B,C,D,E}
3. Mettre à jour les distances des voisins de A :
• d(B)= min(∞,0+1) = 1 et prédécesseur(B) = A
• d(C)= min(∞,0+4) = 4 et prédécesseur(C) = A
4. Choisir le sommet avec la plus petite distance non traité (B) et le marquer comme traité :
• Sommet courant = B
• Q = {C,D,E}
5. Mettre à jour les distances des voisins de B :
• d(C) = min(4,1+2)=3 et prédécesseur(C) = B
• d(D) = min(∞,1+5)=6 et prédécesseur(D) = B
6. Choisir le sommet avec la plus petite distance non traité (C) et le marquer comme traité :
• Sommet courant = C
• Q = {D,E}
7. Mettre à jour les distances des voisins de C :
d(E) = min(∞,3+3) = 6 et prédécesseur(E) = C
8. Choisir le sommet avec la plus petite distance non traité (D) et le marquer comme traité :
• Sommet courant = D
• Q = {E}
9. Mettre à jour les distances des voisins de D :
d(E) = min(6,6+1) = 6 (pas de changement) et prédécesseur(E) = C
10. Choisir le sommet avec la plus petite distance non traité (E) et le marquer comme traité :
• Sommet courant = E
• Q = {}
Finalement, voici la liste des distances et les chemins les plus courts en partant du sommet A:
| Noeud | Valeur | Chemin |
|---|---|---|
| A | 0 | A |
| B | 1 | A → B |
| C | 3 | A → B → C |
| D | 6 | A → B → D |
| E | 6 | A → B → C → E |
Considérez le graphe non orienté suivant :
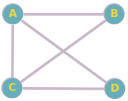
Sommets : A, B, C, D
Arêtes : (A-B), (A-C), (A-D), (B-C), (C-D)
a. Est-ce que ce graphe est biparti ? Justifiez votre réponse.
b. Coloriez le graphe en utilisant le minimum de couleurs possibles. Expliquez votre démarche.
a. Est-ce que ce graphe est biparti ? Justifiez votre réponse.
Un graphe est biparti s'il est possible de diviser les sommets en deux ensembles disjoints U et V tels que chaque arête connecte un sommet de U à un sommet de V, et qu'il n'y a pas d'arête entre deux sommets du même ensemble.
Pour vérifier si un graphe est biparti, on peut utiliser un parcours en largeur (BFS) ou en profondeur (DFS) pour essayer de colorier le graphe avec deux couleurs (disons rouge et bleu) de telle manière que deux sommets adjacents n'ont pas la même couleur. Si c'est possible, le graphe est biparti ; sinon, il ne l'est pas.
Vérification avec un parcours en largeur (BFS) :
1. Initialisation :
• Marquer tous les sommets comme non colorés.
• Choisir un sommet de départ, par exemple A, et le colorier en rouge.
2.Parcours en largeur :
• Colorier les voisins du sommet de départ en bleu.
• Pour chaque sommet colorié en bleu, colorier ses voisins non colorés en rouge.
• Continuer ce processus pour chaque sommet jusqu'à ce que tous les sommets soient colorés ou qu'une contradiction soit trouvée (deux sommets adjacents avec la même couleur).
Application de l'algorithme :
1. Coloration de départ :
• A : rouge
• B,C,D : non colorés
2. Coloration des voisins de A :
B, C, D : bleu
3. Vérification des voisins de B :
• A (rouge) est correct
• C (bleu) → contradiction car B est aussi bleu
Une contradiction a été trouvée. Le graphe n'est donc pas biparti.
b. Coloriez le graphe en utilisant le minimum de couleurs possibles. Expliquez votre démarche.
Pour colorier un graphe en utilisant le minimum de couleurs possibles, on peut utiliser l'algorithme de coloration gloutonne. Cet algorithme attribue à chaque sommet la couleur la plus basse possible qui n'a pas encore été utilisée par ses voisins.
Démarche de coloration gloutonne :
1. Initialisation :
• Marquer tous les sommets comme non colorés.
• Préparer une liste de couleurs disponibles.
2. Choix des couleurs pour chaque sommet :
Pour chaque sommet, attribuer la couleur la plus basse qui n'est pas utilisée par ses voisins.
Application de l'algorithme :
1. Coloration du sommet A :
Couleur : 1 (rouge)
2. Coloration du sommet B :
Voisins colorés : A (rouge)
Couleur disponible : 2 (bleu)
Couleur : 2 (bleu)
3. Coloration du sommet C :
Voisins colorés : A (rouge), B (bleu)
Couleur disponible : 3 (vert)
Couleur : 3 (vert)
4. Coloration du sommet D :
Voisins colorés : A (rouge), C (vert)
Couleur disponible : 2 (bleu)
Couleur : 2 (bleu)
Résultat de la coloration :
| Noeud | Valeur (Couleur) |
|---|---|
| A | 1 (rouge) |
| B | 2 (bleu) |
| C | 3 (vert) |
| D | 2 (bleu) |
1. Algorithme de Kruskal :
Utilisez l'algorithme de Kruskal pour trouver l'arbre couvrant de poids minimum du graphe pondéré suivant :
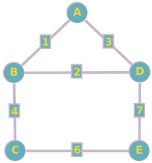
Sommets : A, B, C, D, E
Arêtes pondérées : (A-B, 1), (A-D, 3), (B-C, 4), (B-D, 2), (C-D, 5), (C-E, 6), (D-E, 7)
Listez les arêtes de l'arbre couvrant de poids minimum et donnez son poids total.
2. Algorithme de Prim :
Utilisez l'algorithme de Prim pour trouver l'arbre couvrant de poids minimum en partant du sommet A du même graphe que ci-dessus. Listez les arêtes de l'arbre couvrant de poids minimum et donnez son poids total.
Solution en cours...
Imaginez un réseau social où les utilisateurs sont représentés par des sommets et les amitiés par des arêtes. Voici les utilisateurs et leurs relations :
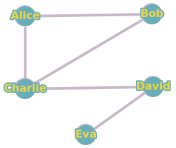
Sommets : Alice, Bob, Charlie, David, Eva
Arêtes : (Alice-Bob), (Alice-Charlie), (Bob-Charlie), (Charlie-David), (David-Eva)
a. Construisez la matrice d'adjacence pour ce graphe.
b. Quel est le degré de chaque utilisateur ?
c. Représentez ce graphe par une liste d'adjacence.
Solution en cours...
Une ville possède un réseau de lignes de bus représenté par un graphe non orienté. Les arrêts de bus sont des sommets et les lignes de bus sont des arêtes.
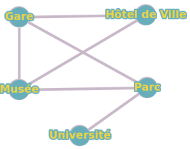
Sommets : Gare, Hôtel de Ville, Musée, Parc, Université
Arêtes : (Gare-Hôtel de Ville), (Gare-Parc), (Hôtel de Ville-Musée), (Musée-Parc), (Parc-Université)
a. Effectuez un parcours en profondeur (DFS) en partant de la Gare. Listez les arrêts dans l'ordre de leur visite.
b. Effectuez un parcours en largeur (BFS) en partant de la Gare. Listez les arrêts dans l'ordre de leur visite.
Solution en cours...
Une compagnie de distribution d'eau veut optimiser ses canalisations pour minimiser les coûts. Les canalisations sont représentées par un graphe pondéré avec les coûts comme poids des arêtes.
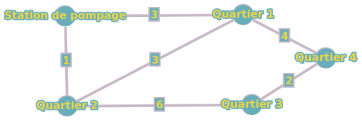
Sommets : Station de pompage, Quartier 1, Quartier 2, Quartier 3, Quartier 4
Arêtes pondérées : (Station de pompage-Quartier 1, 3), (Station de pompage-Quartier 2, 1), (Quartier 1-Quartier 2, 3), (Quartier 2-Quartier 3, 6), (Quartier 3-Quartier 4, 2), (Quartier 4-Quartier 1, 4)
Utilisez l'algorithme de Dijkstra pour trouver le plus court chemin à partir de la Station de pompage vers chaque quartier. Listez les distances et les chemins les plus courts.
Solution en cours...
Une entreprise doit répartir des tâches entre ses employés de manière à ce que deux employés ne travaillent jamais sur une tâche simultanément. Les tâches et les conflits sont représentés par un graphe :
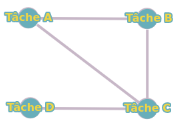
Sommets : Tâche A, Tâche B, Tâche C, Tâche D
Arêtes : (Tâche A-Tâche B), (Tâche A-Tâche C), (Tâche B-Tâche C), (Tâche C-Tâche D)
a. Est-ce que ce graphe est biparti ? Justifiez votre réponse.
b. Coloriez le graphe en utilisant le minimum de couleurs possibles. Expliquez votre démarche.
Solution en cours...
Une entreprise veut connecter ses différents bureaux en utilisant un réseau informatique de manière optimale. Les bureaux et les connexions possibles sont représentés par un graphe pondéré avec les coûts des connexions comme poids des arêtes.
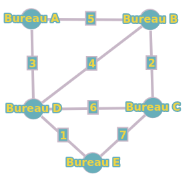
Sommets : Bureau A, Bureau B, Bureau C, Bureau D, Bureau E
Arêtes pondérées : (Bureau A-Bureau B, 5), (Bureau A-Bureau D, 3), (Bureau B-Bureau C, 2), (Bureau B-Bureau D, 4), (Bureau C-Bureau D, 6), (Bureau C-Bureau E, 7), (Bureau D-Bureau E, 1)
a. Utilisez l'algorithme de Kruskal pour trouver l'arbre couvrant de poids minimum. Listez les arêtes de l'arbre couvrant de poids minimum et donnez son poids total.
b. Utilisez l'algorithme de Prim pour trouver l'arbre couvrant de poids minimum en partant du Bureau A. Listez les arêtes de l'arbre couvrant de poids minimum et donnez son poids total.
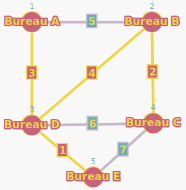
1. Algorithme de Kruskal :
Arêtes sélectionnées :
• (D-E, 1)
• (B-C, 2)
• (A-D, 3)
• (B-D, 4)
Poids total = 1 + 2 + 3 + 4 = 10
2. Algorithme de Prim :
Arêtes sélectionnées :
• (A-D, 3)
• (D-E, 1)
• (B-D, 4)
• (B-C, 2)
Poids total = 3 + 1 + 4 + 2 = 10
Considérez l'arbre binaire de recherche suivant :
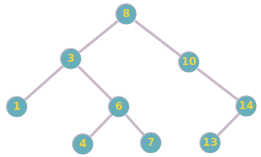
a. Représentez cet arbre sous forme de liste d'adjacence.
b. Quel est le parcours en ordre préfixe (préordre) de cet arbre ?
c. Quel est le parcours en ordre infixe (inordre) de cet arbre ?
d. Quel est le parcours en ordre postfixe (postordre) de cet arbre ?
Solution en cours...
Considérez un arbre binaire de recherche initialement vide. Insérez les éléments suivants dans l'ordre donné : 5, 3, 8, 2, 4, 7, 9.
a. Dessinez l'arbre après chaque insertion.
b. Quel est le parcours en ordre infixe (inordre) de l'arbre final ?
Solution en cours...
Considérez l'arbre binaire de recherche suivant :
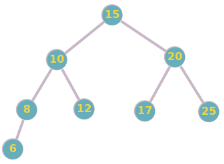
a. Supprimez le nœud avec la valeur 10. Dessinez l'arbre résultant.
b. Supprimez le nœud avec la valeur 15. Dessinez l'arbre résultant.
Solution en cours...
Pour chaque arbre binaire donné ci-dessous, calculez la hauteur de l'arbre.
a. Arbre 1 :

b. Arbre 2 :
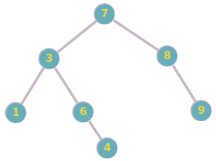
Solution en cours...
Considérez l'arbre binaire suivant :
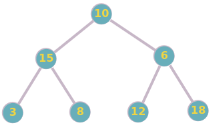
a. Effectuez un parcours en largeur (BFS) de cet arbre. Listez les nœuds dans l'ordre de leur visite.
b. Effectuez un parcours en profondeur en préordre (DFS) de cet arbre. Listez les nœuds dans l'ordre de leur visite.
Solution en cours...
Considérez l'arbre binaire de recherche suivant :
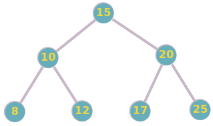
a. Représentez cet arbre sous forme de liste d'adjacence.
b. Quel est le parcours en ordre préfixe (préordre) de cet arbre ?
c. Quel est le parcours en ordre infixe (inordre) de cet arbre ?
d. Quel est le parcours en ordre postfixe (postordre) de cet arbre ?
Solution en cours...
Considérez un arbre binaire de recherche initialement vide. Insérez les éléments suivants dans l'ordre donné : 10, 5, 15, 2, 7, 12, 20.
a. Dessinez l'arbre après chaque insertion.
b. Quel est le parcours en ordre infixe (inordre) de l'arbre final ?
Solution en cours...
Considérez l'arbre binaire de recherche suivant :
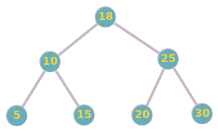
a. Supprimez le nœud avec la valeur 10. Dessinez l'arbre résultant.
b. Supprimez le nœud avec la valeur 18. Dessinez l'arbre résultant.
Solution en cours...
Considérez l'arbre binaire de recherche suivant :
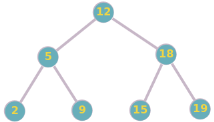
a. Recherchez l'élément 15 dans l'arbre. Expliquez les étapes de la recherche.
b. Recherchez l'élément 7 dans l'arbre. Expliquez les étapes de la recherche.
Solution en cours...
Pour l'arbre binaire de recherche suivant, calculez la hauteur de l'arbre :
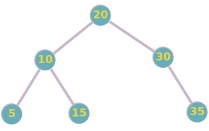
Solution en cours...
Les mathématiques ont souvent la réputation d'être une discipline austère et difficile, mais ...
Read more.Plongez dans l'univers fascinant des suites numériques, où chaque terme révèle des patterns surprenants et des applications pratiques dans les mathématiques et au-delà.
Read more.Découvrez comment les fonctions tissent des liens entre les nombres et les concepts, transformant des idées abstraites en outils puissants pour résoudre des problèmes du quotidien.
Read more.Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !