Exploration des graphes
Un graphe est une structure de données composée de nœuds (ou sommets) et d'arêtes qui décrivent les relations entre ces nœuds. Les graphes sont utilisés pour modéliser des réseaux, des relations sociales, des itinéraires, etc.

graph = {
'A': ['B', 'C'],
'B': ['A', 'C', 'D'],
'C': ['A', 'B', 'D'],
'D': ['B', 'C']
}graph = [
[0, 1, 1, 0],
[1, 0, 1, 1],
[1, 1, 0, 1],
[0, 1, 1, 0]
]def dfs(graph, start):
visited = set()
stack = [start]
while stack:
vertex = stack.pop()
if vertex not in visited:
visited.add(vertex)
stack.extend(set(graph[vertex]) - visited)
return visited
def bfs(graph, start):
visited = set()
queue = [start]
while queue:
vertex = queue.pop(0)
if vertex not in visited:
visited.add(vertex)
queue.extend(set(graph[vertex]) - visited)
return visited
Considérez le graphe suivant :
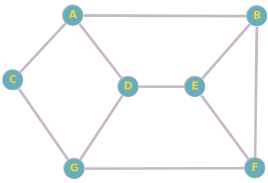
a) Quels sont les sommets adjacents au sommet A ?
b) Quels sont les sommets adjacents au sommet D ?
c) Quels sont les sommets voisins du sommet F ?
d) Quelle est la longueur du plus court chemin entre les sommets A et F ?
e) Quels sont les sommets qui sont à une distance de 2 par rapport au sommet A ?
a) Les sommets adjacents au sommet A sont B,C et D.
b) Les sommets adjacents au sommet D sont A, E et G.
c) Les sommets voisins du sommet F sont B, E et G.
d) Le plus court chemin entre les sommets A et F est A - B - F, donc sa longueur est 2.
e) Les sommets qui sont à une distance de 2 par rapport au sommet A sont E,F et G.Considérez le graphe suivant :
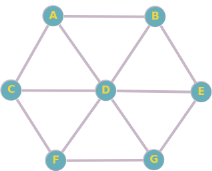
a) Quels sont les sommets adjacents au sommet C ?
b) Quels sont les sommets adjacents au sommet E ?
c) Quels sont les sommets voisins du sommet B ?
d) Quelle est la longueur du plus court chemin entre les sommets A et G ?
a) Les sommets adjacents au sommet C sont A, D et F.
b) Les sommets adjacents au sommet E sont B, D et G.
c) Les sommets voisins du sommet B sont A, D et E.
d) Le plus court chemin entre les sommets A et G est A - D - G, donc sa longueur est 2.
Considérez le graphe suivant :
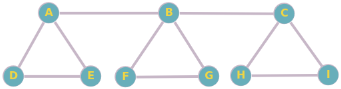
a) Quels sont les sommets adjacents au sommet B ?
b) Quels sont les sommets adjacents au sommet F ?
c) Quels sont les sommets voisins du sommet G ?
d) Quel est le nombre de chemins de longueur 2 entre les sommets A et I ?
e) Quel est le chemin le plus court entre les sommets D et G ?
a) Les sommets adjacents au sommet B sont A, C, F et G.
b) Les sommets adjacents au sommet F sont B et G.
c) Les sommets voisins du sommet G sont B et H.
d) Le nombre de chemins de longueur 2 entre les sommets A et I est 2 (A - B - C et A - B - G). e) Le chemin le plus court entre les sommets D et G est D - E - F - G, donc sa longueur est 3.
Considérez le graphe suivant :
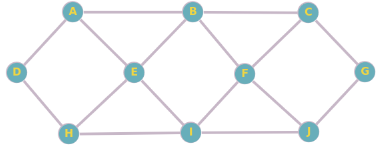
a) Quels sont les sommets adjacents au sommet E ?
b) Quels sont les sommets adjacents au sommet I ?
c) Quels sont les sommets voisins du sommet F ?
d) Quel est le nombre de chemins de longueur 3 entre les sommets A et G ?
e) Quel est le chemin le plus court entre les sommets D et J ?
a) Les sommets adjacents au sommet E sont A, B, H et I.
b) Les sommets adjacents au sommet I sont E, F, H et J.
c) Les sommets voisins du sommet F sont B, C, E, G et I.
d) Le nombre de chemins de longueur 3 entre les sommets A et G est 4 (A - B - C - G, A - B - F - G, A - D - E - F - G et A - D - H - I - J). e) Le chemin le plus court entre les sommets D et J est D - H - I - J, donc sa longueur est 3.
Écrivez une fonction Python qui prend en entrée un graphe non orienté sous forme de liste d'adjacence et qui renvoie le nombre de sommets dans le graphe.
def nombre_de_sommets(graphe):
return len(graphe)
# Exemple d'utilisation
graphe = [[1, 2], [0, 2, 3], [0, 1, 3], [1, 2]]
print(nombre_de_sommets(graphe)) # Résultat : 4Écrivez une fonction Python qui prend en entrée un graphe non orienté sous forme de liste d'adjacence et qui renvoie le degré d'un sommet donné.
def degre_sommet(graphe, sommet):
return len(graphe[sommet])
# Exemple d'utilisation
graphe = [[1, 2], [0, 2, 3], [0, 1, 3], [1, 2]]
sommet = 1
print(degre_sommet(graphe, sommet)) # Résultat : 3Écrivez une fonction Python qui prend en entrée un graphe non orienté sous forme de liste d'adjacence et qui renvoie tous les voisins d'un sommet donné.
def voisins_sommet(graphe, sommet):
return graphe[sommet]
# Exemple d'utilisation
graphe = [[1, 2], [0, 2, 3], [0, 1, 3], [1, 2]]
sommet = 2
print(voisins_sommet(graphe, sommet)) # Résultat : [0, 1, 3]Écrivez une fonction Python qui prend en entrée un graphe non orienté sous forme de liste d'adjacence et qui renvoie True si deux sommets donnés sont adjacents, sinon False.
def sont_adjacents(graphe, sommet1, sommet2):
return sommet2 in graphe[sommet1]
# Exemple d'utilisation
graphe = [[1, 2], [0, 2, 3], [0, 1, 3], [1, 2]]
sommet1 = 0
sommet2 = 2
print(sont_adjacents(graphe, sommet1, sommet2)) # Résultat : TrueLes mathématiques ont souvent la réputation d'être une discipline austère et difficile, mais ...
Read more.Plongez dans l'univers fascinant des suites numériques, où chaque terme révèle des patterns surprenants et des applications pratiques dans les mathématiques et au-delà.
Read more.Découvrez comment les fonctions tissent des liens entre les nombres et les concepts, transformant des idées abstraites en outils puissants pour résoudre des problèmes du quotidien.
Read more.Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !