Exploration des piles et files en python
Une pile est une structure de données linéaire qui permet d'ajouter et de retirer des éléments selon le principe du dernier entré, premier sorti (LIFO - Last-In-First-Out). Les opérations de base sur une pile sont l'empilement (push) pour ajouter un élément et le dépilement (pop) pour retirer le dernier élément ajouté.
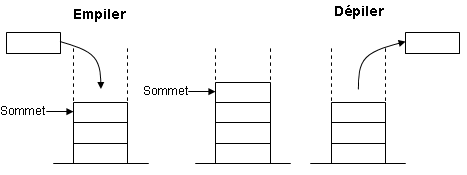
En Python, vous pouvez représenter une pile en utilisant une liste. Les opérations d'empilement et de dépilement peuvent être réalisées en utilisant les méthodes append() et pop() de la liste, respectivement.
Voici un exemple de code Python pour créer une pile vide et réaliser des opérations d'empilement et de dépilement :
| Exemple de code | Simulateur |
|---|---|
|
|
Les piles sont couramment utilisées pour résoudre des problèmes qui impliquent un ordre de traitement inversé, ou lorsqu'il est nécessaire de revenir en arrière dans une séquence d'actions.
Par exemple, voici un exemple de code Python qui utilise une pile pour inverser l'ordre des éléments d'une liste :
def inverser_liste(liste):
pile = []
for element in liste:
pile.append(element)
liste_inverse = []
while pile:
element = pile.pop()
liste_inverse.append(element)
return liste_inverse
ma_liste = [1, 2, 3, 4, 5]
liste_inverse = inverser_liste(ma_liste)
print(liste_inverse) # Affiche : [5, 4, 3, 2, 1]
Une file est une structure de données linéaire qui permet d'ajouter des éléments à l'arrière et de retirer les éléments à l'avant selon le principe du premier entré, premier sorti (FIFO - First-In-First-Out). Les opérations de base sur une file sont l'ajout (enqueue) pour ajouter un élément à l'arrière et la suppression (dequeue) pour retirer l'élément à l'avant.

En Python, vous pouvez représenter une file en utilisant une liste. Les opérations d'ajout et de suppression peuvent être réalisées en utilisant les méthodes append() pour ajouter un élément à l'arrière et pop(0) pour retirer l'élément à l'avant de la liste.
Voici un exemple de code Python pour créer une file vide et réaliser des opérations d'ajout et de suppression :
| Exemple de code | Simulateur |
|---|---|
|
|
Les files sont couramment utilisées pour modéliser des processus basés sur une file d'attente, tels que la gestion des tâches, les requêtes réseau, etc.
Par exemple, voici un exemple de code Python qui utilise une file pour simuler un processus de traitement de commandes :
def traiter_commandes(commandes):
file = []
for commande in commandes:
file.append(commande)
while file:
commande = file.pop(0)
print("Traitement de la commande :", commande)
# Effectuer le traitement de la commande ici
# Exemple d'utilisation
commandes = ["Commande 1", "Commande 2", "Commande 3"]
traiter_commandes(commandes)
Ce code simule le traitement de commandes en les plaçant dans une file, puis en les traitant dans l'ordre d'arrivée.
Les piles et les files sont des structures de données essentielles en informatique. La compréhension de leurs principes de fonctionnement et de leurs opérations de base est fondamentale pour de nombreux problèmes et algorithmes.
Écrivez une classe Python qui implémente une pile (stack) utilisant une liste comme structure de données sous-jacente. La pile doit prendre en charge les opérations suivantes :
empiler(element): ajoute un élément au sommet de la pile.depiler(): retire et renvoie l'élément situé au sommet de la pile.est_vide(): renvoie True si la pile est vide, False sinon.class Pile:
def __init__(self):
self.elements = []
def empiler(self, element):
self.elements.append(element)
def depiler(self):
if self.est_vide():
raise IndexError("La pile est vide.")
return self.elements.pop()
def est_vide(self):
return len(self.elements) == 0
# Exemple d'utilisation
pile = Pile()
pile.empiler(1)
pile.empiler(2)
pile.empiler(3)
print(pile.depiler()) # Résultat : 3
print(pile.depiler()) # Résultat : 2
print(pile.est_vide()) # Résultat : False
print(pile.depiler()) # Résultat : 1
print(pile.est_vide()) # Résultat : True
Écrivez une fonction Python qui prend en entrée une expression mathématique sous forme de chaîne de caractères (contenant des nombres, des opérateurs et des parenthèses) et qui renvoie True si les parenthèses de l'expression sont correctement équilibrées, False sinon.
def parentheses_equilibrees(expression):
pile = Pile()
for caractere in expression:
if caractere == '(':
pile.empiler(caractere)
elif caractere == ')':
if pile.est_vide():
return False
pile.depiler()
return pile.est_vide()
# Exemple d'utilisation
expression1 = "(2 + 3) * (4 - 1)"
expression2 = "((2 + 3) * (4 - 1)"
expression3 = "(2 + 3) * (4 - 1))"
print(parentheses_equilibrees(expression1)) # Résultat : True
print(parentheses_equilibrees(expression2)) # Résultat : False
print(parentheses_equilibrees(expression3)) # Résultat : False Écrivez une fonction Python qui prend en entrée une expression mathématique sous forme de chaîne de caractères en notation infixée et qui renvoie l'expression équivalente en notation postfixée (notation polonaise inverse).
def infix_to_postfix(expression):
precedence = {'+': 1, '-': 1, '*': 2, '/': 2} # Précédence des opérateurs
postfix = [] # Liste pour stocker l'expression postfixée
stack = Pile() # Pile pour gérer les opérateurs
for caractere in expression:
if caractere.isdigit():
postfix.append(caractere) # Ajoute les opérandes directement à l'expression postfixée
elif caractere == '(':
stack.empiler(caractere) # Empile les parenthèses ouvrantes
elif caractere == ')':
while not stack.est_vide() and stack.depiler() != '(':
postfix.append(stack.depiler()) # Dépile les opérateurs jusqu'à la parenthèse ouvrante correspondante
elif caractere in precedence:
while not stack.est_vide() and stack.elements[-1] != '(' and precedence[caractere] <= precedence[stack.elements[-1]]:
postfix.append(stack.depiler()) # Dépile les opérateurs ayant une précédence supérieure ou égale
stack.empiler(caractere) # Empile l'opérateur courant
while not stack.est_vide():
postfix.append(stack.depiler()) # Dépile tous les opérateurs restants
return ''.join(postfix)
# Exemple d'utilisation
expression = "((2+3)*(4-1))/5"
resultat = infix_to_postfix(expression)
print(resultat) # Résultat : "23+41-*5/"
Écrivez une classe Python qui implémente une pile (stack) avec la possibilité d'effectuer une opération de rotation sur les k éléments supérieurs de la pile. La rotation déplace les k éléments supérieurs vers le bas de la pile.
class PileAvecRotation(Pile):
def rotation(self, k):
elements = []
for _ in range(k):
elements.append(self.depiler()) # Retire les k éléments supérieurs de la pile
sommet = self.depiler() # Récupère l'élément suivant (nouveau sommet)
while not self.est_vide():
elements.append(self.depiler()) # Retire les autres éléments de la pile
for _ in range(k):
self.empiler(elements.pop()) # Réinsère les k éléments supérieurs (dans l'ordre inverse)
self.empiler(sommet) # Réinsère le sommet
# Exemple d'utilisation
pile = PileAvecRotation()
pile.empiler(1)
pile.empiler(2)
pile.empiler(3)
pile.empiler(4)
pile.empiler(5)
pile.rotation(3)
print(pile.depiler()) # Résultat : 3
print(pile.depiler()) # Résultat : 2
print(pile.depiler()) # Résultat : 1
print(pile.depiler()) # Résultat : 5
print(pile.depiler()) # Résultat : 4
Écrivez une fonction Python qui prend en entrée une liste de caractères représentant une expression mathématique en notation postfixée (notation polonaise inverse) et qui renvoie True si l'expression est syntaxiquement valide et peut être évaluée, False sinon.
def expression_valide(expression):
pile = Pile()
for caractere in expression:
if caractere.isdigit():
pile.empiler(caractere) # Empile les opérandes
elif caractere in '+-*/':
if len(pile.elements) < 2:
return False # Pas assez d'opérandes pour l'opérateur courant
pile.depiler()
pile.depiler()
pile.empiler('') # Empile un espace réservé pour le résultat
return len(pile.elements) == 1
# ExempleLa réponse a été tronquée. Voici la suite de l'exemple d'utilisation pour l'exercice 3 :
expression1 = ['4', '5', '+', '2', '*']
expression2 = ['4', '5', '+', '*']
expression3 = ['4', '5', '+', '2', '*', '*']
print(expression_valide(expression1)) # Résultat : True
print(expression_valide(expression2)) # Résultat : False
print(expression_valide(expression3)) # Résultat : False
Écrivez une classe Python qui implémente une file (queue) utilisant une liste comme structure de données sous-jacente. La file doit prendre en charge les opérations suivantes :
enfiler(element): ajoute un élément à la fin de la file.defiler(element): retire et renvoie l'élément en tête de la file.est_vide(): renvoie True si la file est vide, False sinon.class File:
def __init__(self):
self.elements = []
def enfiler(self, element):
self.elements.append(element)
def defiler(self):
if self.est_vide():
raise IndexError("La file est vide.")
return self.elements.pop(0)
def est_vide(self):
return len(self.elements) == 0
# Exemple d'utilisation
file = File()
file.enfiler(1)
file.enfiler(2)
file.enfiler(3)
print(file.defiler()) # Résultat : 1
print(file.defiler()) # Résultat : 2
print(file.est_vide()) # Résultat : False
print(file.defiler()) # Résultat : 3
print(file.est_vide()) # Résultat : True
Écrivez une fonction Python qui prend en entrée une liste d'entiers et un entier k, et qui renvoie une nouvelle liste contenant les moyennes glissantes des sous-listes de taille k. La moyenne glissante d'une liste est la moyenne de ses éléments consécutifs.
def moyennes_glissantes(liste, k):
file = File()
resultats = []
somme = 0
for i, valeur in enumerate(liste):
if i < k:
somme += valeur
else:
resultats.append(somme / k)
somme -= file.defiler()
somme += valeur
file.enfiler(valeur)
resultats.append(somme / k) # Ajoute la dernière moyenne glissante
return resultats
# Exemple d'utilisation
liste = [1, 2, 3, 4, 5, 6, 7, 8, 9]
k = 3
resultats = moyennes_glissantes(liste, k)
print(resultats) # Résultat : [2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0]
Écrivez une fonction Python qui prend en entrée une chaîne de caractères contenant une séquence d'opérations sur une file, et qui renvoie le nombre d'éléments restants dans la file après l'exécution de toutes les opérations. Les opérations possibles sont :
E: ajoute un élément à la fin de la file.D: retire l'élément situé au début de la file.def nombre_elements_restants(operations):
file = File()
for operation in operations:
if operation == 'E':
file.enfiler(None) # Ajoute un élément fictif à la file
elif operation == 'D':
if file.est_vide():
raise IndexError("La file est vide.")
file.defiler()
return len(file.elements)
# Exemple d'utilisation
operations = "EDDEED"
resultat = nombre_elements_restants(operations)
print(resultat) # Résultat : 2
Considérez le labyrinthe représenté sous forme de graphe :
laby = {1: [5, 2], 2: [1, 3, 6], 3: [2], 4: [8], 5: [1], 6: [2, 7], 7: [11, 6, 8], 8: [12, 7, 4], 9: [10],
10: [11, 9, 14], 11: [7, 10], 12: [8], 13: [14], 14: [13, 15, 10], 15: [16, 14], 16: [15]}
Implémentez une fonction parcours_profondeur(graphe, départ) qui effectue un parcours en profondeur du labyrinthe à partir du sommet de départ et renvoie la liste des sommets visités dans l'ordre.
def parcours_profondeur(graphe, départ):
pile = [départ]
visités = []
while pile:
sommet = pile.pop()
if sommet not in visités:
visités.append(sommet)
voisins = graphe[sommet]
pile.extend(voisins)
return visités
# Exemple d'utilisation
parcours = parcours_profondeur(laby, 1)
print(parcours)
# Résultat :
[1, 2, 3, 6, 7, 11, 10, 9, 14, 15, 16, 13, 4, 8, 12, 5]
Utilisez la fonction parcours_profondeur que vous avez implémentée pour trouver un chemin entre deux sommets du labyrinthe. Par exemple, recherchez un chemin entre le sommet 1 et le sommet 16.
def recherche_chemin(graphe, départ, arrivée):
pile = [(départ, [départ])]
while pile:
sommet, chemin = pile.pop()
if sommet == arrivée:
return chemin
voisins = graphe[sommet]
for voisin in voisins:
if voisin not in chemin:
pile.append((voisin, chemin + [voisin]))
return None
# Exemple d'utilisation
chemin = recherche_chemin(laby, 1, 16)
print(chemin)
# Résultat :
[1, 2, 3, 6, 7, 11, 10, 14, 13, 15, 16]
ⓘ Si un chemin existe entre le sommet de départ et le sommet d'arrivée, la fonction renvoie la liste des sommets constituant le chemin. Sinon, elle renvoie None.
Considérez le graphe représentant un réseau social avec les relations d'amitié suivantes :
graph = {
'Alice': ['Bob', 'Charlie'],
'Bob': ['Alice', 'Dave'],
'Charlie': ['Alice', 'Eve'],
'Dave': ['Bob'],
'Eve': ['Charlie', 'Frank'],
'Frank': ['Eve']
}Implémentez une fonction parcours_profondeur(graphe, départ) qui réalise un parcours en profondeur du graphe à partir du sommet de départ et renvoie la liste des sommets visités dans l'ordre.
def parcours_profondeur(graphe, départ):
pile = [départ]
visités = []
while pile:
sommet = pile.pop()
if sommet not in visités:
visités.append(sommet)
voisins = graphe[sommet]
pile.extend(voisins)
return visités
# Exemple d'utilisation
parcours = parcours_profondeur(graph, 'Alice')
print(parcours)
# Résultat :
['Alice', 'Charlie', 'Eve', 'Frank', 'Bob', 'Dave']
Utilisez la fonction parcours_profondeur que vous avez implémentée pour trouver un chemin entre deux sommets du graphe. Par exemple, recherchez un chemin entre 'Alice' et 'Frank'.
def recherche_chemin(graphe, départ, arrivée):
pile = [(départ, [départ])]
while pile:
sommet, chemin = pile.pop()
if sommet == arrivée:
return chemin
voisins = graphe[sommet]
for voisin in voisins:
if voisin not in chemin:
pile.append((voisin, chemin + [voisin]))
return None
# Exemple d'utilisation
chemin = recherche_chemin(graph, 'Alice', 'Frank')
print(chemin)
# Résultat :
['Alice', 'Charlie', 'Eve', 'Frank']
ⓘ Si un chemin existe entre le sommet de départ et le sommet d'arrivée, la fonction renvoie la liste des sommets constituant le chemin. Sinon, elle renvoie None.
créer une fonction somme(p) qui calcule la somme des entiers présents dans une pile.
def somme(p):
# Vérifie si la pile est vide
if not p:
return 0
# Retire l'élément du sommet de la pile
element = p.pop()
# Calcule la somme récursive des éléments restants
total = element + somme(p)
# Ajoute l'élément retiré à la pile pour maintenir l'intégrité de celle-ci
p.append(element)
return total
# Exemple d'utilisation
pile = [1, 2, 3, 4, 5]
resultat = somme(pile)
print("La somme des entiers dans la pile est :", resultat)
créer une fonction incremente(𝑛) qui empile les entiers de 1 à n.
def incremente(n, pile=None):
# Initialise la pile la première fois que la fonction est appelée
if pile is None:
pile = []
# Cas de base : si n est zéro, on retourne la pile
if n <= 0:
return pile
# Appel récursif avec n-1
incremente(n - 1, pile)
# Empile l'entier n
pile.append(n)
return pile
# Exemple d'utilisation
n = 5
pile = incremente(n)
print("La pile avec les entiers de 1 à", n, "est :", pile)
créer une fonction produit(p) qui calcule le produit des entiers présents dans une pile.
def produit(p):
# Vérifie si la pile est vide
if not p:
return 1 # Le produit de rien est 1 (élément neutre pour la multiplication)
# Retire l'élément du sommet de la pile
element = p.pop()
# Calcule le produit récursif des éléments restants
total = element * produit(p)
# Remet l'élément retiré pour conserver l'intégrité de la pile
p.append(element)
return total
# Exemple d'utilisation
pile = [2, 3, 4]
resultat = produit(pile)
print("Le produit des entiers dans la pile est :", resultat)
Que renvoie produit(incremente(𝑛)), si n est un entier ?
La fonction `produit(incremente(n))` renvoie le produit des entiers de 1 à n.
Explication :
1. `incremente(n)` :
Cette fonction empile les entiers de 1 à n dans une pile.
Par exemple, si `n` est 5, la pile sera `[1, 2, 3, 4, 5]`.
2. `produit(p)` :
Cette fonction calcule le produit des entiers présents dans la pile.
En utilisant l'exemple précédent, avec une pile `[1, 2, 3, 4, 5]`,
le produit calculé sera `1 * 2 * 3 * 4 * 5`, ce qui donne 120.
Conclusion :
En résumé, `produit(incremente(n))` renvoie `n!` (n factoriel),
qui est le produit de tous les entiers de 1 à n..
créer un prédicat sorted_stack(p) qui détermine si les entiers dans la pile sont ordonnés en ordre croissant, avec le plus petit en haut.
def sorted_stack(p):
# Cas de base : si la pile est vide ou contient un seul élément, elle est considérée comme triée
if len(p) <= 1:
return True
# Retire l'élément du sommet de la pile
top = p.pop()
# Vérifie si le reste de la pile est trié
is_sorted = sorted_stack(p)
# Vérifie si l'élément du sommet est supérieur ou égal au nouvel élément du sommet
if not is_sorted or (p and top > p[-1]):
# Remet l'élément retiré et renvoie False
p.append(top)
return False
# Remet l'élément retiré pour préserver l'intégrité de la pile
p.append(top)
return True
# Exemple d'utilisation
pile = [1, 2, 3, 4, 5]
print("La pile est triée :", sorted_stack(pile))
pile2 = [3, 1, 4, 2]
print("La pile est triée :", sorted_stack(pile2))
créer une fonction inverse_stack(p) qui renvoie une pile avec les éléments dans l'ordre inverse.
def inverse_stack(p):
# Cas de base : si la pile est vide, on renvoie une pile vide
if not p:
return []
# Retire l'élément du sommet de la pile
top = p.pop()
# Appel récursif pour inverser le reste de la pile
reversed_stack = inverse_stack(p)
# Ajoute l'élément retiré à la fin de la pile inversée
reversed_stack.append(top)
return reversed_stack
# Exemple d'utilisation
pile = [1, 2, 3, 4, 5]
pile_inversee = inverse_stack(pile)
print("La pile inversée est :", pile_inversee)
Les mathématiques ont souvent la réputation d'être une discipline austère et difficile, mais ...
Read more.Plongez dans l'univers fascinant des suites numériques, où chaque terme révèle des patterns surprenants et des applications pratiques dans les mathématiques et au-delà.
Read more.Découvrez comment les fonctions tissent des liens entre les nombres et les concepts, transformant des idées abstraites en outils puissants pour résoudre des problèmes du quotidien.
Read more.Abonnez-vous maintenant et recevez notre newsletter hebdomadaire avec des matériaux éducatifs, de nouveaux cours, des articles intéressants, des livres populaires et bien plus encore !