madamasterclass.com
-
Connexion
Connexion
Introduction à la Programmation Fonctionnelle
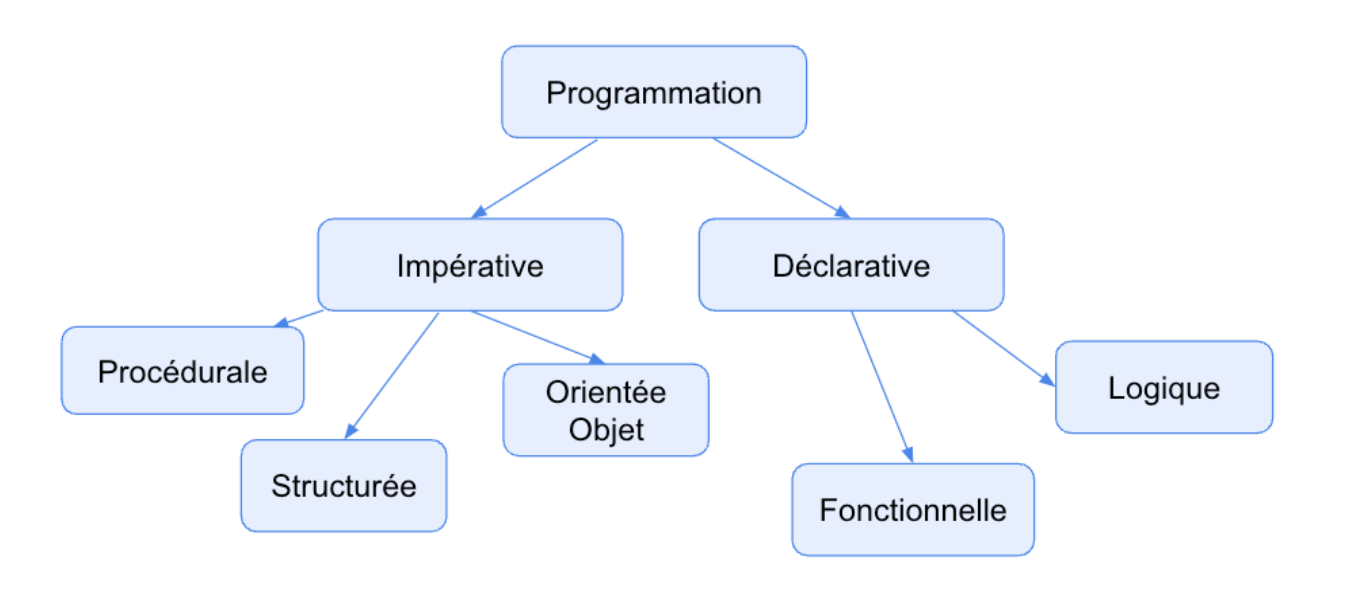
La programmation fonctionnelle est un paradigme de programmation qui traite le calcul comme l'évaluation de fonctions mathématiques et évite les changements d'état et les données mutables. En Python, la programmation fonctionnelle est soutenue par des fonctionnalités intégrées et des bibliothèques qui facilitent son utilisation.
Éducation
def appliquer(fonction, valeur):
return fonction(valeur)map, filter et reduce.carre = lambda x: x ** 2
resultat = appliquer(carre, 5) # Retourne 25map applique une fonction à tous les éléments d'un itérable.filter filtre les éléments d'un itérable en fonction d'une condition.reduce applique une fonction cumulativement aux éléments d'un itérable.from functools import reduce
liste = [1, 2, 3, 4]
resultat_map = list(map(carre, liste)) # [1, 4, 9, 16]
resultat_filter = list(filter(lambda x: x % 2 == 0, liste)) # [2, 4]
resultat_reduce = reduce(lambda x, y: x + y, liste) # 10La programmation fonctionnelle en Python permet d'écrire un code clair, concis et modulaire. En utilisant des concepts tels que les fonctions d'ordre supérieur, l'immuabilité et les fonctions lambda, vous pouvez adopter un style de programmation qui favorise la réutilisabilité et la simplicité.
Soit la fonction \( f(x) = x^2 + 2x + 1 \).
1. Écrire une fonction Python qui prend un entier \( n \) et retourne \( f(n) \).
2. Utiliser cette fonction pour calculer \( f(3) \) et \( f(5) \).
3. Écrire une fonction d'ordre supérieur qui applique \( f \) à une liste de nombres et retourne une nouvelle liste avec les résultats.
4. Tester cette fonction avec la liste \([1, 2, 3, 4, 5]\).
Considérons la suite de Fibonacci, définie par \( F(0) = 0 \), \( F(1) = 1 \) et \( F(n) = F(n-1) + F(n-2) \) pour \( n \geq 2 \).
1. Écrire une fonction récursive pour calculer \( F(n) \).
2. Écrire une fonction qui utilise map pour générer les 10 premiers termes de la suite de Fibonacci.
3. Utiliser filter pour extraire les termes pairs des 10 premiers termes de la suite.
Écrire un programme qui effectue les opérations suivantes :
1. Écrire une fonction qui prend une liste de chaînes et retourne une nouvelle liste avec chaque chaîne en majuscules.
2. Écrire une fonction qui prend une liste de chaînes et retourne une nouvelle liste avec les longueurs de chaque chaîne.
3. Combiner les deux fonctions pour obtenir une liste de tuples, où chaque tuple contient une chaîne en majuscules et sa longueur.
Soit la fonction \( g(x) = 3x - 5 \).
1. Écrire une fonction Python qui prend un entier \( n \) et retourne \( g(n) \).
2. Utiliser cette fonction pour calculer \( g(-2) \) et \( g(10) \).
3. Écrire une fonction qui applique \( g \) à une liste de nombres et retourne une nouvelle liste contenant les résultats.
4. Tester cette fonction avec la liste \([-1, 0, 1, 2, 3]\).
On considère une liste de mots :
\[ \text{mots} = ["hello", "world", "python", "functional", "programming"] \]
1. Écrire une fonction qui prend cette liste et retourne une nouvelle liste contenant uniquement les mots qui contiennent la lettre 'o'.
2. Écrire une fonction qui retourne la longueur de chaque mot de la liste d'origine.
3. Combiner les deux fonctions pour créer une liste de tuples où chaque tuple contient un mot contenant 'o' et sa longueur.
Vous travaillez sur un projet qui nécessite de manipuler des températures.
1. Écrire une fonction qui convertit une température en Celsius en Fahrenheit, avec la formule \( F = C \times \frac{9}{5} + 32 \).
2. Écrire une fonction qui prend une liste de températures en Celsius et retourne une liste de ces températures converties en Fahrenheit.
3. Tester votre fonction avec la liste de températures \([0, 10, 20, 30, 40]\).
Dans une application de gestion de produits, vous devez traiter les prix.
1. Écrire une fonction qui applique une remise de 20% à un prix donné.
2. Écrire une fonction qui prend une liste de prix et retourne une nouvelle liste avec les prix après application de la remise.
3. Tester votre fonction avec la liste de prix \([100, 200, 300, 400, 500]\).
Vous développez un système de gestion de notes d'étudiants.
1. Écrire une fonction qui calcule la moyenne d'une liste de notes.
2. Écrire une fonction qui prend une liste de listes de notes et retourne une nouvelle liste avec les moyennes de chaque étudiant.
3. Tester votre fonction avec la liste \([[10, 12, 14], [15, 20, 18], [8, 7, 6]]\).
Dans une application de filtrage de données, vous devez traiter une liste d'âges.
1. Écrire une fonction qui filtre les âges pour ne garder que ceux qui sont supérieurs ou égaux à 18.
2. Tester cette fonction avec la liste d'âges \([15, 18, 20, 17, 25, 30]\).
Vous travaillez sur un projet de traitement de chaînes de caractères.
1. Écrire une fonction qui retourne la première lettre de chaque mot d'une phrase donnée.
2. Écrire une fonction qui prend une phrase et retourne une nouvelle phrase formée par ces premières lettres.
3. Tester cette fonction avec la phrase "La programmation fonctionnelle est puissante".
Les mathématiques ont souvent la réputation d'être une discipline austère et difficile, mais ...
Read more.Plongez dans l'univers fascinant des suites numériques, où chaque terme révèle des patterns surprenants et des applications pratiques dans les mathématiques et au-delà.
Read more.Découvrez comment les fonctions tissent des liens entre les nombres et les concepts, transformant des idées abstraites en outils puissants pour résoudre des problèmes du quotidien.
Read more.
