Question 1

La fonction \( f(x) = \cos(x) \) est :

• a) Impaire
• b) Paire
• c) Ni paire ni impaire
• d) Périodique mais impaire

Question 2

La dérivée de \( f(x) = \frac{1}{x^2 + 1} \) est :

• a) \( \frac{2x}{(x^2 + 1)^2} \)
• b) \( -\frac{2x}{(x^2 + 1)^2} \)
• c) \( -\frac{1}{(x^2 + 1)^2} \)
• d) \( \frac{1}{(x^2 + 1)^2} \)

Question 3

Le domaine de définition de \( f(x) = \frac{1}{x-2} \) est :

• a) \( \mathbb{R} \setminus \{2\} \)
• b) \( \mathbb{R} \setminus \{0\} \)
• c) \( ]0; +\infty[ \)
• d) \( \mathbb{R} \)

Question 4

La fonction \( f(x) = x^3 - 3x \) admet un maximum local en :

• a) \( x = 0 \)
• b) \( x = \sqrt{3} \)
• c) \( x = -1 \)
• d) \( x = -\sqrt{3} \)

Question 5

La pente de la tangente à \( f(x) = \sqrt{x} \) en \( x = 4 \) est :

• a) \( \frac{1}{4} \)
• b) \( \frac{1}{2} \)
• c) \( \frac{1}{\sqrt{4}} \)
• d) \( \frac{1}{2\sqrt{4}} \)

Question 6

Si \( f'(x) > 0 \) sur \( ]-2;5[ \), alors la fonction \( f \) est :

• a) Décroissante sur \( ]-2;5[ \)
• b) Constante sur \( ]-2;5[ \)
• c) Croissante sur \( ]-2;5[ \)
• d) Strictement décroissante sur \( ]-2;5[ \)

Question 7

Le taux d'accroissement de \( f(x) = x^2 \) entre \( x = 1 \) et \( x = 3 \) est :

• a) 2
• b) 4
• c) 5
• d) 8

Question 8

Si \( f'(x) < 0 \) sur un intervalle, cela signifie que :

• a) \( f \) est croissante
• b) \( f \) est décroissante
• c) \( f \) est constante
• d) \( f \) est convexe

Question 9

La fonction \( f(x) = \sin(x) + \cos(x) \) est :

• a) Périodique de période \( \pi \)
• b) Périodique de période \( 2\pi \)
• c) Non périodique
• d) Paire

Question 10

La courbe de \( f(x) = x^2 - 4 \) coupe l'axe des abscisses en :

• a) \( x = 2 \)
• b) \( x = -2 \)
• c) \( x = \pm 2 \)
• d) \( x = 0 \)

Question 11

La fonction \( f(x) = x^3 \) admet un centre de symétrie en :

• a) \( (0; 0) \)
• b) \( (1; 1) \)
• c) \( (-1; -1) \)
• d) Aucun

Question 12

L'équation de la tangente à \( f(x) = x^2 \) au point \( x = 1 \) est :

• a) \( y = x \)
• b) \( y = 2x - 1 \)
• c) \( y = 2x + 1 \)
• d) \( y = x^2 \)

On considère la fonction \(P\) définie sur ℝ par \(P(x) = x^2 + 4x + 3\).

1. Étudier le signe de la fonction \(P\) sur ℝ.
2. On considère la fonction \( f \) définie sur ]−2; +∞[ par : \[ f(x) = \frac{x^2 + x - 1}{x + 2} \] et on note 𝐶𝑓 sa courbe représentative dans un repère orthogonal du plan. On admet que \( f \) est dérivable sur ]−2; +∞[.
   1. Montrer que pour tout réel x ∈ ]−2; +∞[, \[ f'(x) = \frac{P(x)}{(x+2)^2} \] où \(f'\) est la fonction dérivée de \( f \).
   2. Étudier le signe de \(f'(x)\) sur ]−2; +∞[ et construire le tableau de variations de \( f \).
3. Donner le minimum de \( f \) sur ]−2; +∞[ et la valeur pour laquelle il est atteint (valeurs exactes).
4. Déterminer le coefficient directeur de la tangente 𝑇 à 𝐶𝑓 au point d'abscisse 2.

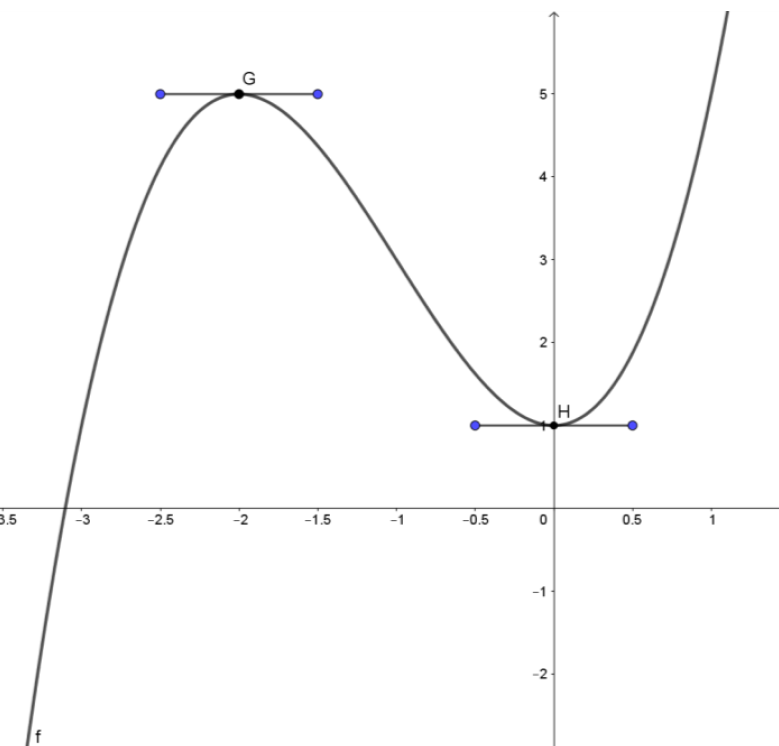
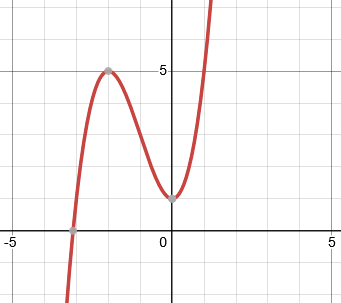
La courbe ci-dessous représente une fonction \( f \) définie et dérivable sur ℝ.

1. Déterminer \( f(0) \), \( f(−2) \), \( f'(0) \) et \( f'(−2) \).
2. On admet que pour tout réel \( x \), \( f(x) \) peut s'écrire sous la forme : \[ f(x) = ax^3 + bx^2 + cx + d \]
   1. Donner une expression de \( f'(x) \).
   2. Déterminer les valeurs des réels \( c \) et \( d \).
   3. Déterminer deux équations que vérifient les réels \( a \) et \( b \).
   4. En déduire que \( f(x) = x^3 + 3x^2 + 1 \).

Question 1

La dérivée de \( f(x) = x^2 \cdot \cos(x) \) est :

• a) \( 2x\cos(x) - x^2\sin(x) \)
• b) \( 2x\cos(x) + \sin(x) \)
• c) \( \cos(x) - 2x\sin(x) \)
• d) \( 2x\sin(x) + \cos(x) \)

Question 2

L'équation de la tangente à \( f(x) = x^3 \) au point d'abscisse \( x = 1 \) est :

• a) \( y = 3x + 1 \)
• b) \( y = 3x - 2 \)
• c) \( y = 3x - 2 \)
• d) \( y = x^3 \)

Question 3

Le domaine de définition de \( f(x) = \sqrt{3 - x} \) est :

• a) \( ]-\infty ; 3] \)
• b) \( [3 ; +\infty[ \)
• c) \( ]-\infty ; 0] \)
• d) \( \mathbb{R} \)

Question 4

Si \( f'(x) = (x - 2)(x + 1) \), alors la fonction \( f \) est :

• a) Croissante sur \( ]-\infty; -1[ \cup ]2; +\infty[ \)
• b) Décroissante sur \( ]-1; 2[ \)
• c) Minimum local en \( x = -1 \)
• d) Maximum global en \( x = 2 \)

Question 5

Les fonctions \( f(x) = x^2 \) et \( g(x) = 2x \) se coupent en :

• a) \( x = 0 \) et \( x = 2 \)
• b) \( x = 1 \) et \( x = 2 \)
• c) \( x = -2 \) et \( x = 2 \)
• d) Une seule fois

Question 6

Le taux d'accroissement de \( f(x) = \frac{1}{x} \) entre \( x = 1 \) et \( x = 2 \) est :

• a) \( -1 \)
• b) \( -\frac{1}{2} \)
• c) \( -\frac{1}{4} \)
• d) \( -\frac{1}{2} \cdot \frac{1}{2} \)

Question 7

La fonction \( f(x) = x^2 + 1 \) est :

• a) Paire
• b) Impaire
• c) Ni paire ni impaire
• d) Périodique

Question 8

La courbe de la fonction \( f(x) = (x - 1)^2 \) admet un axe de symétrie :

• a) L'axe des abscisses
• b) La droite \( x = 0 \)
• c) La droite \( x = 1 \)
• d) La droite \( y = x \)

Question 9

La fonction \( f(x) = -x^3 + 3x \) admet un centre de symétrie en :

• a) \( (0; 0) \)
• b) \( (1; 2) \)
• c) Aucun
• d) \( (0; 3) \)

Question 10

Si \( f'(x) > 0 \) sur un intervalle, alors :

• a) \( f \) est constante
• b) \( f \) est décroissante
• c) \( f \) est croissante
• d) \( f \) est négative

Question 11

Une fonction dérivable sur \( \mathbb{R} \) a un minimum local en \( x = 2 \). Cela signifie :

• a) \( f'(2) = 0 \) et \( f''(2) > 0 \)
• b) \( f'(2) > 0 \) et \( f''(2) > 0 \)
• c) \( f'(2) = 0 \) et \( f''(2) < 0 \)
• d) \( f'(2) \ne 0 \)

Question 12

La dérivée de \( f(x) = \frac{x}{x+1} \) est :

• a) \( \frac{1}{x+1} \)
• b) \( \frac{1}{(x+1)^2} \)
• c) \( \frac{1}{(x+1)^2} \cdot x \)
• d) \( \frac{1}{(x+1)^2} \cdot (1 - x) \)

Soit la fonction \( f \) définie sur \( ]-3; +\infty[ \) par \( f(x) = \frac{x^2 + kx + 2}{x + 3} \) où \( k \) est un réel.

1. Étude préliminaire
   1. Pour \( k = 4 \), étudier le signe du polynôme \( P(x) = x^2 + 4x + 2 \).
   2. En déduire les coordonnées du point d'intersection de \( C_f \) avec l'axe des ordonnées lorsque \( k = 4 \).
2. Dérivabilité
   1. Montrer que pour tout \( k \) réel, \( f \) est dérivable sur \( ]-3; +\infty[ \) et exprimer \( f'(x) \).
   2. Pour \( k = 1 \), déterminer les abscisses des points où la tangente est horizontale.
3. Problème de tangente
   1. Pour \( k = 2 \), montrer que la tangente au point d'abscisse \( -1 \) passe par l'origine.
   2. Existe-t-il une valeur de \( k \) pour laquelle la tangente en \( x = 0 \) a pour coefficient directeur \( 1 \) ?
4. Optimisation
   1. Pour \( k = 3 \), déterminer le minimum de \( f \) sur \( ]-2; +\infty[ \).
   2. Montrer que ce minimum est atteint pour \( x = \sqrt{3} - 3 \).

La courbe ci-dessous représente une fonction \( f \) définie et dérivable sur \( \mathbb{R} \).

1. Lecture graphique
   1. Déterminer \( f(0) \), \( f(-1) \), \( f(2) \), \( f'(-1) \) et \( f'(2) \).
   2. La tangente au point d'abscisse \( 1 \) passe-t-elle par \( D(3;-2) \) ? Justifier graphiquement.
2. Modélisation
   1. On suppose \( f(x) = ax^3 + bx^2 + cx + d \). Écrire le système d'équations vérifié par \( a,b,c,d \).
   2. Montrer que \( d = 1 \) et \( c = -3 \).
   3. Résoudre le système pour déterminer \( a \) et \( b \).
3. Analyse complémentaire
   1. Vérifier que \( f'(x) = 3x^2 - 2x - 3 \).
   2. Étudier les variations de \( f \) et dresser son tableau de variations.
   3. Déterminer l'équation de la tangente au point d'inflexion.

Question 1

La dérivée de \( f(x) = \sqrt{x^2 + 1} \) est :

• a) \( \frac{1}{2\sqrt{x^2 + 1}} \)
• b) \( \frac{2x}{2\sqrt{x^2 + 1}} \)
• c) \( \frac{x}{\sqrt{x^2 + 1}} \)
• d) \( \frac{2}{\sqrt{x^2 + 1}} \)

Question 2

L’équation de la tangente à \( f(x) = \sin(x) \) en \( x = 0 \) est :

• a) \( y = x \)
• b) \( y = \cos(0)x \)
• c) \( y = 0 \)
• d) \( y = \sin(0) + \cos(0)(x - 0) \)

Question 3

Le taux d’accroissement de \( f(x) = x^2 \) entre \( x = -1 \) et \( x = 3 \) est :

• a) 2
• b) 3
• c) 4
• d) 5

Question 4

La fonction \( f(x) = \frac{x+2}{x^2 - 1} \) est définie sur :

• a) \( \mathbb{R} \setminus \{-1, 1\} \)
• b) \( \mathbb{R} \setminus \{0\} \)
• c) \( \mathbb{R} \setminus \{1\} \)
• d) \( \mathbb{R} \)

Question 5

La période de la fonction \( f(x) = \cos(2x) \) est :

• a) \( \pi \)
• b) \( 2\pi \)
• c) \( \frac{\pi}{2} \)
• d) \( \frac{2}{\pi} \)

Question 6

Simplifier \( (x^3)^2 \cdot x^{-4} \) :

• a) \( x^2 \)
• b) \( x^4 \)
• c) \( x^6 \)
• d) \( x^5 \)

Question 7

La dérivée de \( f(x) = e^{x^3} \) est :

• a) \( 3x^2 e^{x^3} \)
• b) \( x^2 e^x \)
• c) \( e^{3x^2} \)
• d) \( 3x e^{x^2} \)

Question 8

Le point d’intersection de la courbe de \( f(x) = 4x - 7 \) avec l’axe des ordonnées est :

• a) \( (0 ; -7) \)
• b) \( (4 ; 0) \)
• c) \( (-7 ; 0) \)
• d) \( (0 ; 4) \)

Question 9

L’axe de symétrie de la fonction \( f(x) = (x - 5)^2 \) est :

• a) \( x = 5 \)
• b) \( x = 0 \)
• c) \( x = -5 \)
• d) \( x = 2.5 \)

Question 10

La fonction \( f(x) = -x^2 + 4x \) admet un maximum local pour :

• a) \( x = 2 \)
• b) \( x = 0 \)
• c) \( x = 4 \)
• d) \( x = -2 \)

Question 11

Si \( f'(x) > 0 \) sur un intervalle, alors \( f \) est :

• a) croissante sur cet intervalle
• b) décroissante sur cet intervalle
• c) constante
• d) discontinue

Question 12

La formule de \( \cos(2x) \) en fonction de \( \cos(x) \) est :

• a) \( 2\cos^2(x) - 1 \)
• b) \( \cos^2(x) - \sin^2(x) \)
• c) \( 1 - 2\sin^2(x) \)
• d) Toutes les réponses précédentes sont vraies

Soit la fonction \( f \) définie sur \( ]-1; +\infty[ \) par \( f(x) = \frac{2x^2 + kx - 1}{x + 1} \) où \( k \) est un réel.

1. Cas particulier (k = 3)
   1. Montrer que \( f'(x) = \frac{2x^2 + 4x + 4}{(x + 1)^2} \) pour \( k = 3 \).
   2. Démontrer que \( f \) admet un minimum local en \( x = -2 \).
2. Problème de tangente
   1. Pour \( k = 0 \), déterminer l'équation de la tangente au point d'abscisse 1.
   2. Cette tangente coupe-t-elle l'axe des ordonnées en \( y = -3 \) ?
3. Optimisation (nouveau)
   1. Déterminer \( k \) pour que le minimum de \( f \) soit atteint en \( x = 0 \).
   2. Calculer ce minimum pour la valeur de \( k \) trouvée.
4. Analyse graphique
   1. Tracer l'allure de la courbe pour \( k = 2 \) en indiquant les éléments remarquables.
   2. Déterminer graphiquement le nombre de solutions de \( f(x) = m \) selon \( m \).

La courbe ci-dessous représente une fonction \( g \) définie et dérivable sur \( \mathbb{R} \).

1. Lecture graphique améliorée
   1. Déterminer \( g(0) \), \( g(-2) \), \( g(1) \), \( g'(-2) \), \( g'(1) \) et \( g''(0) \).
   2. La dérivée seconde s'annule-t-elle ailleurs qu'en \( x = 0 \) ?
2. Modélisation avancée
   1. On suppose \( g(x) = ax^4 + bx^3 + cx^2 + dx + e \). Écrire le système vérifié par les coefficients.
   2. Montrer que \( e = 1 \) et \( d = 0 \).
   3. Ajouter une condition pour garantir le point d'inflexion en \( x = 0 \).
3. Étude complète (nouveau)
   1. Déterminer les extremums locaux et leur nature.
   2. Étudier la convexité de \( g \) et préciser les abscisses des points d'inflexion.
4. Problème ouvert
   1. Existe-t-il une tangente à la courbe passant par \( D(3;10) \) ?
   2. Si oui, combien y en a-t-il et quelles sont leurs équations ?

Barème indicatif :

• QCM : 0,5 point par question (6 points)
• Exercice 1 : 7 points
• Exercice 2 : 7 points

Question 1

La dérivée de \( f(x) = x^2 + 5x \) est :

• a) \( 2x + 5 \)
• b) \( 2x + 10 \)
• c) \( x^2 + 5 \)
• d) \( 2x \)

Question 2

L’équation de la tangente à \( f(x) = x^2 \) en \( x = -1 \) est :

• a) \( y = -2x - 1 \)
• b) \( y = -2x + 1 \)
• c) \( y = 2x + 1 \)
• d) \( y = -x^2 \)

Question 3

Le taux d’accroissement de \( f(x) = 3x \) entre \( x = 1 \) et \( x = 4 \) est :

• a) 1
• b) 3
• c) 9
• d) 12

Question 4

Le domaine de définition de \( f(x) = \frac{1}{x^2 - 4} \) est :

• a) \( \mathbb{R} \setminus \{-2, 2\} \)
• b) \( \mathbb{R} \setminus \{0\} \)
• c) \( \mathbb{R} \)
• d) \( \mathbb{R}^+ \)

Question 5

La fonction \( f(x) = x^2 \) est :

• a) Paire
• b) Impaire
• c) Ni paire ni impaire
• d) Constante

Question 6

La simplification de \( \frac{x^5 \cdot x^2}{x^3} \) donne :

• a) \( x^4 \)
• b) \( x^5 \)
• c) \( x^6 \)
• d) \( x^7 \)

Question 7

La formule de \( \sin(a - b) \) est :

• a) \( \sin(a)\sin(b) - \cos(a)\cos(b) \)
• b) \( \sin(a)\cos(b) - \cos(a)\sin(b) \)
• c) \( \sin(a) - \sin(b) \)
• d) \( \sin(a + b) \)

Question 8

La dérivée de \( f(x) = e^{2x} \) est :

• a) \( 2e^{2x} \)
• b) \( e^{x^2} \)
• c) \( x \cdot e^{2x} \)
• d) \( e^x \)

Question 9

Le point d’intersection de \( f(x) = x^2 - 4 \) avec l’axe des abscisses est :

• a) \( x = -2 \) et \( x = 2 \)
• b) \( x = 0 \)
• c) \( x = -4 \)
• d) Aucun

Question 10

La fonction \( f(x) = (x - 3)^2 \) est symétrique par rapport à :

• a) l’axe \( x = 3 \)
• b) l’axe \( x = 0 \)
• c) l’axe \( x = -3 \)
• d) l’axe \( y = 3 \)

Question 11

La fonction \( f(x) = x^2 - 6x + 5 \) atteint un minimum en :

• a) \( x = 3 \)
• b) \( x = 2 \)
• c) \( x = -3 \)
• d) \( x = 5 \)

Question 12

Si \( f'(x) < 0 \) sur un intervalle, alors \( f \) est :

• a) Constante
• b) Décroissante
• c) Croissante
• d) Nulle

Soit la fonction \( f \) définie sur \( ]-2; +\infty[ \) par \( f(x) = \frac{x^2 - x - 6}{x + 2} \).

1. Étude préliminaire
   1. Factoriser le numérateur \( x^2 - x - 6 \).
   2. En déduire une expression simplifiée de \( f(x) \) pour \( x \neq -2 \).
2. Dérivée et variations
   1. Calculer \( f'(x) \) et montrer que \( f'(x) = \frac{x^2 + 4x + 4}{(x + 2)^2} \).
   2. Étudier le signe de \( f'(x) \) et dresser le tableau de variations complet.
3. Tangentes et extremums
   1. Déterminer les coordonnées du point où la tangente est horizontale.
   2. Donner l'équation de la tangente au point d'abscisse \( 0 \).
4. Problème graphique
   1. Déterminer les points d'intersection avec les axes.
   2. Tracer l'allure de la courbe en y faisant apparaître les éléments trouvés.

On considère la fonction \( g \) définie sur \( \mathbb{R} \) par \( g(x) = x^3 - 6x^2 + 9x + 1 \).

1. Dérivée et points critiques
   1. Calculer \( g'(x) \) et factoriser l'expression obtenue.
   2. Déterminer les abscisses des points où la tangente est horizontale.
2. Étude des variations
   1. Dresser le tableau de variations complet de \( g \).
   2. Préciser la nature des extremums locaux.
3. Problèmes de tangentes
   1. Déterminer l'équation de la tangente au point d'abscisse \( 2 \).
   2. Montrer que cette tangente passe par le point \( (1, 3) \).
4. Points particuliers
   1. Déterminer le point d'inflexion de la courbe.
   2. Résoudre \( g(x) = 1 \) par le calcul et interpréter graphiquement.

📋 Informations pratiques

• Durée : 3 heures
• Calculatrice non autorisée
• Barème : QCM (6 pts) + Exercice 1 (7 pts) + Exercice 2 (7 pts) = 20 pts
• Toutes les réponses doivent être justifiées sauf pour le QCM

Question 1

La dérivée de \( f(x) = x^4 - 3x^2 \) est :

• a) \( 4x^3 - 6x \)
• b) \( 3x^3 - 2x \)
• c) \( 4x^2 - 6 \)
• d) \( 2x - 6x \)

Question 2

L’équation de la tangente à la courbe de \( f(x) = \frac{1}{x} \) au point d’abscisse \( x = 1 \) est :

• a) \( y = -x + 2 \)
• b) \( y = -x + 1 \)
• c) \( y = -x \)
• d) \( y = x + 1 \)

Question 3

Le taux d’accroissement de \( f(x) = \frac{1}{x} \) entre \( x = 1 \) et \( x = 2 \) est :

• a) \( -\frac{1}{2} \)
• b) \( \frac{1}{2} \)
• c) \( -1 \)
• d) \( \frac{1}{3} \)

Question 4

La fonction \( f(x) = \sqrt{x - 2} \) est définie sur :

• a) \( ]2 ; +\infty[ \)
• b) \( \mathbb{R} \setminus \{2\} \)
• c) \( \mathbb{R} \)
• d) \( [2 ; +\infty[ \)

Question 5

La fonction \( f(x) = \tan(x) \) est :

• a) Paire
• b) Impaire et périodique
• c) Ni paire ni impaire
• d) Constante

Question 6

La simplification de \( \frac{(2x^3 + 3x^2)^2}{x^4} \) donne :

• a) \( 4x^2 + 12x + 9 \)
• b) \( 4x^4 + 12x^3 + 9x^2 \)
• c) \( 4x^2 + 12x + 9x^{-2} \)
• d) \( 4x^2 + 6x + 9 \)

Question 7

La formule de \( \sin(a + b) \) est :

• a) \( \sin(a)\cos(b) + \cos(a)\sin(b) \)
• b) \( \sin(a)\cos(b) - \cos(a)\sin(b) \)
• c) \( \sin(a) + \sin(b) \)
• d) \( \sin(a - b) \)

Question 8

Si \( f'(x) > 0 \) sur un intervalle, alors \( f \) est :

• a) constante
• b) décroissante
• c) croissante
• d) n’a pas d’extremum

Question 9

La fonction \( f(x) = (x + 1)^2 \) est symétrique par rapport à :

• a) l’axe \( x = 0 \)
• b) l’axe \( x = 1 \)
• c) l’axe \( x = -1 \)
• d) l’axe \( y = -1 \)

Question 10

Le point d’intersection de la courbe de \( f(x) = 2x + 3 \) avec l’axe des ordonnées est :

• a) \( (0 ; 3) \)
• b) \( (2 ; 0) \)
• c) \( (3 ; 0) \)
• d) \( (0 ; 2) \)

Question 11

La fonction \( f(x) = -x^2 + 2x + 1 \) admet un maximum en :

• a) \( x = -1 \)
• b) \( x = 1 \)
• c) \( x = 2 \)
• d) \( x = 0 \)

Question 12

La dérivée de \( f(x) = e^{3x^2} \) est :

• a) \( 6x e^{3x^2} \)
• b) \( e^{3x^2} \)
• c) \( 3x^2 e^{3x^2} \)
• d) \( 6x^2 e^x \)

Soit la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = x^3 - 3x^2 + 4 \).

1. Dérivation et variations
   1. Calculer \( f'(x) \) et déterminer les points critiques (où \( f'(x) = 0 \)).
   2. Étudier le signe de \( f'(x) \) et dresser le tableau de variations complet.
   3. Identifier les extremums locaux et préciser s'ils sont globaux.
2. Tangentes et symétrie
   1. Déterminer l'équation de la tangente au point d'abscisse \( x = 1 \).
   2. Montrer que le point \( A(1, 2) \) est un centre de symétrie de \( \mathcal{C}_f \).
   3. Déterminer les coordonnées du point où la tangente a une pente de 9.
3. Problème géométrique
   1. Résoudre \( f(x) = 0 \) et en déduire les points d'intersection avec les axes.
   2. Étudier la parité de \( f \) (justifier).

Soit la fonction \( g \) définie sur \( \mathbb{R}\setminus\{-1\} \) par \( g(x) = \frac{2x^2 - x}{x + 1} \).

1. Étude préliminaire
   1. Déterminer le domaine de définition \( \mathcal{D}_g \).
   2. Calculer \( g(0) \), \( g(2) \) et \( g(-2) \).
   3. Étudier la parité de \( g \).
2. Dérivation et applications
   1. Calculer \( g'(x) \) et simplifier l'expression.
   2. Déterminer les abscisses des points à tangente horizontale.
   3. Calculer le taux d'accroissement entre \( x = 1 \) et \( x = 3 \).
3. Problème de tangente
   1. Écrire l'équation de la tangente au point d'abscisse \( x = 0 \).
   2. Déterminer si le point \( B(1, 0.5) \) appartient à cette tangente.

Question 1

La dérivée de \( f(x) = \frac{1}{x^2} \) est :

• a) \( -2x^{-3} \)
• b) \( \frac{2}{x^3} \)
• c) \( \frac{1}{2x} \)
• d) \( -\frac{2}{x^3} \)

Question 2

L’équation de la tangente à \( f(x) = x^2 - 1 \) au point d’abscisse \( x = 1 \) est :

• a) \( y = 2x - 1 \)
• b) \( y = x^2 - 1 \)
• c) \( y = x + 1 \)
• d) \( y = 2x - 2 \)

Question 3

Le taux d’accroissement de \( f(x) = x^2 \) entre \( x = 2 \) et \( x = 5 \) est :

• a) 7
• b) 8
• c) 9
• d) 10

Question 4

Le domaine de définition de \( f(x) = \sqrt{x - 1} \) est :

• a) \( \mathbb{R} \)
• b) \( [1 ; +\infty[ \)
• c) \( ]1 ; +\infty[ \)
• d) \( ]-\infty ; 1] \)

Question 5

La fonction \( f(x) = \sin(x) \) est :

• a) Paire et périodique
• b) Impaire et périodique
• c) Paire uniquement
• d) Ni paire ni périodique

Question 6

La simplification de \( e^x \cdot e^{-2x} \) donne :

• a) \( e^{-x^2} \)
• b) \( e^{-x} \)
• c) \( e^x \cdot (-2x) \)
• d) \( -e^x + e^{-2x} \)

Question 7

La formule de \( \cos(a + b) \) est :

• a) \( \cos(a)\cos(b) + \sin(a)\sin(b) \)
• b) \( \cos(a)\cos(b) - \sin(a)\sin(b) \)
• c) \( \cos(a) + \cos(b) \)
• d) \( \cos(a + b) = \cos(a - b) \)

Question 8

Si \( f'(x) < 0 \) sur un intervalle, alors \( f \) est :

• a) Constante
• b) Croissante
• c) Décroissante
• d) Strictement positive

Question 9

La fonction \( f(x) = (x - 2)^2 \) est symétrique par rapport à :

• a) l’axe vertical \( x = 2 \)
• b) l’axe horizontal \( y = 2 \)
• c) l’origine
• d) l’axe \( x = 0 \)

Question 10

Les courbes de \( f(x) = x^2 \) et \( g(x) = 2x + 3 \) se croisent pour :

• a) \( x = -1 \) et \( x = 3 \)
• b) \( x = 1 \) et \( x = 2 \)
• c) \( x = -3 \) et \( x = 1 \)
• d) \( x = -1 \) et \( x = 2 \)

Question 11

La fonction \( f(x) = -x^2 + 6x - 5 \) atteint son maximum pour :

• a) \( x = 5 \)
• b) \( x = 3 \)
• c) \( x = 2 \)
• d) \( x = -3 \)

Question 12

La dérivée de \( f(x) = e^{\sin(x)} \) est :

• a) \( \cos(x) \cdot e^{\sin(x)} \)
• b) \( \sin(x) \cdot e^{\cos(x)} \)
• c) \( e^{\cos(x)} \cdot \cos(x) \)
• d) \( \cos(x) + e^{\sin(x)} \)

Soit la fonction \( h \) définie sur \( \mathbb{R} \) par \( h(x) = -x^3 + 6x^2 - 9x + 2 \).

1. Analyse fondamentale
   1. Déterminer le domaine de définition de \( h \).
   2. Calculer les limites de \( h \) en \( -\infty \) et \( +\infty \).
   3. Étudier la parité de \( h \).
2. Dérivation et variations
   1. Calculer \( h'(x) \) et résoudre \( h'(x) = 0 \).
   2. Dresser le tableau de variations complet de \( h \).
   3. Identifier et caractériser les extremums locaux.
3. Tangentes et points remarquables
   1. Déterminer l'équation de la tangente au point d'abscisse \( x = 2 \).
   2. Montrer que le point \( C(2, 0) \) est un point d'inflexion pour \( \mathcal{C}_h \).
   3. Déterminer les points d'intersection de \( \mathcal{C}_h \) avec l'axe des abscisses.

Soit la fonction \( k \) définie sur \( \mathbb{R}\setminus\{2\} \) par \( k(x) = \frac{x^2 - 4x + 3}{x - 2} \).

1. Étude préliminaire
   1. Déterminer le domaine de définition \( \mathcal{D}_k \).
   2. Calculer \( k(0) \), \( k(1) \) et \( k(3) \).
   3. Vérifier si \( k \) admet un axe ou un centre de symétrie.
2. Analyse des variations
   1. Calculer \( k'(x) \) sous forme simplifiée.
   2. Étudier le signe de \( k'(x) \) et dresser le tableau de variations.
   3. Déterminer les abscisses des extremums locaux.
3. Problèmes de tangentes
   1. Déterminer l'équation de la tangente au point d'abscisse \( x = 1 \).
   2. Calculer le coefficient directeur de la tangente au point d'abscisse \( x = 0 \).
   3. Déterminer les points où la tangente est parallèle à la droite \( y = x \).

Question 1

La dérivée de \( f(x) = 5x^3 - 2x^2 \) est :

• a) \( 15x^2 - 2x \)
• b) \( 15x^2 - 4x \)
• c) \( 5x^2 - 4x \)
• d) \( 5x^3 - 2x \)

Question 2

La tangente à \( f(x) = x^2 \) au point d'abscisse \( x = 1 \) a pour équation :

• a) \( y = 2x - 1 \)
• b) \( y = x^2 \)
• c) \( y = 2x \)
• d) \( y = x + 1 \)

Question 3

Le taux d'accroissement de \( f(x) = \sqrt{x} \) entre \( x = 1 \) et \( x = 4 \) est :

• a) \( \frac{3}{2} \)
• b) \( \frac{1}{3} \)
• c) \( \frac{1}{2} \)
• d) \( \frac{2}{3} \)

Question 4

Le domaine de définition de \( f(x) = \frac{1}{x-3} \) est :

• a) \( \mathbb{R} \setminus \{3\} \)
• b) \( \mathbb{R} \setminus \{0\} \)
• c) \( ]0 ; +\infty[ \)
• d) \( \mathbb{R} \)

Question 5

La fonction \( f(x) = \cos(x) \) est :

• a) Paire et périodique
• b) Impaire et périodique
• c) Paire et non périodique
• d) Ni paire ni périodique

Question 6

La simplification de \( \frac{e^{2x}}{e^x} \) donne :

• a) \( e^2 \)
• b) \( e^x \)
• c) \( 2e^x \)
• d) \( x \cdot e^x \)

Question 7

Les fonctions \( f(x) = x^2 \) et \( g(x) = 4x - 3 \) se coupent pour :

• a) \( x = 1 \) et \( x = 3 \)
• b) \( x = 2 \) et \( x = 4 \)
• c) \( x = -1 \) et \( x = 4 \)
• d) Une seule fois

Question 8

La dérivée de \( f(x) = \tan(x) \) est :

• a) \( \sec^2(x) \)
• b) \( \cos^2(x) \)
• c) \( \sin^2(x) \)
• d) \( \tan(x)\cdot\sec(x) \)

Question 9

La fonction \( f(x) = -x^2 + 2x \) admet un maximum local en :

• a) \( x = 1 \)
• b) \( x = 0 \)
• c) \( x = -1 \)
• d) Aucun

Question 10

Si \( f'(x) > 0 \) sur \( ]-1 ; 2[ \), alors \( f \) est :

• a) Constante sur \( ]-1 ; 2[ \)
• b) Croissante sur \( ]-1 ; 2[ \)
• c) Décroissante sur \( ]-1 ; 2[ \)
• d) Convexe sur \( ]-1 ; 2[ \)

Question 11

La fonction \( f(x) = (x-3)^2 \) est symétrique par rapport à :

• a) L’axe vertical \( x = 3 \)
• b) L’axe horizontal \( y = 3 \)
• c) L’origine
• d) L’axe \( x = 0 \)

Question 12

La dérivée de \( f(x) = e^{\cos(x)} \) est :

• a) \( -\sin(x)\cdot e^{\cos(x)} \)
• b) \( \cos(x)\cdot e^{\cos(x)} \)
• c) \( \sin(x)\cdot e^{x} \)
• d) \( e^{\cos(x)} \cdot \cos(x) \)

Soit la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = x^3 - 6x^2 + 9x + 1 \).

1. Étude préliminaire
   1. Calculer \( f(0) \), \( f(1) \) et \( f(3) \).
   2. Déterminer les limites de \( f \) en \( -\infty \) et \( +\infty \).
   3. Étudier la parité de \( f \).
2. Analyse des variations
   1. Calculer \( f'(x) \) et déterminer les points critiques.
   2. Dresser le tableau de variations complet de \( f \).
   3. Identifier les extremums locaux et préciser leur nature.
3. Problèmes de tangentes
   1. Déterminer l'équation de la tangente au point d'abscisse \( x = 2 \).
   2. Montrer que la tangente en \( x = 1 \) passe par l'origine du repère.
   3. Déterminer les abscisses des points où la tangente a un coefficient directeur égal à 3.
4. Problème géométrique
   1. Résoudre \( f(x) = 1 \) et interpréter graphiquement.
   2. Déterminer les coordonnées du point d'intersection de \( \mathcal{C}_f \) avec l'axe des ordonnées.

Soit la fonction \( g \) définie sur \( \mathbb{R}\setminus\{1\} \) par \( g(x) = \frac{x^2 + 2x}{x - 1} \).

1. Étude de base
   1. Déterminer le domaine de définition \( \mathcal{D}_g \).
   2. Calculer \( g(-1) \), \( g(0) \) et \( g(2) \).
   3. Étudier la parité de \( g \).
2. Dérivation et applications
   1. Calculer \( g'(x) \) sous forme simplifiée.
   2. Déterminer les abscisses des points à tangente horizontale.
   3. Étudier les variations de \( g \) et dresser son tableau de variations.
3. Tangentes et symétrie
   1. Déterminer l'équation de la tangente au point d'abscisse \( x = 0 \).
   2. Montrer que le point \( A(1, -3) \) est centre de symétrie pour \( \mathcal{C}_g \).
   3. Déterminer les points où la tangente est parallèle à la droite \( y = 2x \).

Question 1

La dérivée de \( f(x) = \frac{x^2 + 1}{x} \) est :

• a) \( \frac{2x \cdot x - (x^2 + 1)}{x^2} \)
• b) \( \frac{x^2 - 1}{x^2} \)
• c) \( \frac{2x - 1}{x} \)
• d) \( \frac{2x}{x} \)

Question 2

La tangente à \( f(x) = \cos(x) \) en \( x = 0 \) a pour équation :

• a) \( y = x \)
• b) \( y = 1 \)
• c) \( y = -x + 1 \)
• d) \( y = \cos(x) \)

Question 3

Le taux d'accroissement de \( f(x) = x^2 \) entre \( x = 1 \) et \( x = 3 \) est :

• a) 4
• b) 3
• c) 2
• d) 5

Question 4

La forme simplifiée de \( e^x \cdot e^{3x} \) est :

• a) \( e^{x + 3} \)
• b) \( e^{3x} \)
• c) \( e^{4x} \)
• d) \( e^{x^3} \)

Question 5

La dérivée de \( f(x) = \sin(x)\cos(x) \) est :

• a) \( \cos^2(x) - \sin^2(x) \)
• b) \( \cos(x)\sin(x) \)
• c) \( \sin(2x) \)
• d) \( \cos^2(x) + \sin^2(x) \)

Question 6

Le domaine de définition de \( f(x) = \sqrt{3 - x} \) est :

• a) \( ]-\infty ; 3] \)
• b) \( [3 ; +\infty[ \)
• c) \( ]-\infty ; 3[ \)
• d) \( \mathbb{R} \)

Question 7

La fonction \( f(x) = \sin(x) \) est :

• a) Paire et périodique
• b) Impaire et périodique
• c) Impaire mais non périodique
• d) Ni paire ni périodique

Question 8

Si \( f'(x) = (x - 1)(x + 2) \), alors \( f \) est :

• a) Croissante sur \( ]-\infty ; -2[ \cup ]1 ; +\infty[ \)
• b) Décroissante sur \( ]-\infty ; -2[ \cup ]1 ; +\infty[ \)
• c) Croissante sur \( ]-2 ; 1[ \)
• d) Constante

Question 9

La courbe de \( f(x) = (x - 2)^2 \) est symétrique par rapport à :

• a) \( x = 2 \)
• b) \( x = 0 \)
• c) \( y = 2 \)
• d) \( x = -2 \)

Question 10

Les fonctions \( f(x) = x^2 \) et \( g(x) = 2x + 3 \) ont un point d’intersection en :

• a) \( x = -1 \) et \( x = 3 \)
• b) \( x = 0 \) et \( x = 3 \)
• c) \( x = 1 \) et \( x = 3 \)
• d) \( x = -3 \) et \( x = 1 \)

Question 11

La fonction \( f(x) = -x^2 + 4x \) atteint son maximum pour :

• a) \( x = -2 \)
• b) \( x = 0 \)
• c) \( x = 2 \)
• d) \( x = 4 \)

Question 12

La simplification de \( \ln(e^{x^2}) \) est :

• a) \( x^2 \)
• b) \( \ln(x^2) \)
• c) \( e^{\ln(x^2)} \)
• d) \( 2x \)

Soit la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = \frac{1}{4}x^4 - 2x^2 + x + 1 \).

1. Étude préliminaire
   1. Calculer \( f(-2) \), \( f(0) \) et \( f(2) \).
   2. Déterminer le comportement de \( f \) lorsque \( x \) tend vers \( -\infty \) et \( +\infty \).
   3. Étudier la parité de \( f \).
2. Dérivation et variations
   1. Calculer \( f'(x) \) et déterminer les points critiques.
   2. Étudier le signe de \( f'(x) \) et dresser le tableau de variations.
   3. Identifier et caractériser les extremums locaux.
3. Tangentes et points particuliers
   1. Déterminer l'équation de la tangente au point d'abscisse \( x = 1 \).
   2. Trouver les abscisses des points où la tangente est horizontale.
   3. Déterminer si le point \( A(0,1) \) appartient à une tangente horizontale.

Soit la fonction \( g \) définie sur \( \mathbb{R}\setminus\{3\} \) par \( g(x) = \frac{x^3 - 5x}{x - 3} \).

1. Analyse de base
   1. Déterminer le domaine de définition \( \mathcal{D}_g \) et discuter des implications sur le comportement de \( g(x) \) aux alentours de \( x=3 \).
   2. Calculer \( g(-1) \), \( g(0) \) et \( g(2) \).
   3. Étudier la parité de \( g \).
2. Dérivation et étude
   1. Calculer \( g'(x) \) sous forme simplifiée.
   2. Déterminer les points où la dérivée s'annule.
   3. Dresser le tableau complet des variations de \( g \).
3. Problèmes de tangentes
   1. Déterminer l'équation de la tangente en \( x = 2 \).
   2. Trouver les points où la tangente a un coefficient directeur égal à 4.
   3. Montrer que \( \mathcal{C}_g \) admet un centre de symétrie.
4. Intersections et positions
   1. Déterminer les points d'intersection avec les axes.
   2. Étudier la position relative de \( \mathcal{C}_g \) par rapport à sa tangente en \( x = 0 \).

Question 1

La dérivée de \( f(x) = x^2 \cdot e^x \) est :

• a) \( 2xe^x \)
• b) \( (2x + x^2)e^x \)
• c) \( (x^2 + e^x)^2 \)
• d) \( e^x + 2x \)

Question 2

La simplification de \( \frac{\sin(x)}{\cos(x)} \cdot \cos(x) \) donne :

• a) \( \tan(x) \)
• b) \( \sin(x)\cos(x) \)
• c) \( \sin(x) \)
• d) \( 1 \)

Question 3

L’équation de la tangente à \( f(x) = \frac{1}{x} \) au point d’abscisse \( x = 1 \) est :

• a) \( y = -x + 2 \)
• b) \( y = \frac{1}{x} \)
• c) \( y = -\frac{1}{x^2} \)
• d) \( y = -x + 1 \)

Question 4

Le domaine de définition de \( f(x) = \frac{1}{\sqrt{x - 2}} \) est :

• a) \( ]-\infty ; 2[ \)
• b) \( [2 ; +\infty[ \)
• c) \( ]2 ; +\infty[ \)
• d) \( \mathbb{R} \setminus \{2\} \)

Question 5

Soit \( f(x) = \frac{1}{x^2} \). La fonction est :

• a) Strictement croissante sur \( \mathbb{R}^* \)
• b) Strictement décroissante sur \( \mathbb{R}^* \)
• c) Décroissante sur \( ]0 ; +\infty[ \) et croissante sur \( ]-\infty ; 0[ \)
• d) Croissante sur \( ]0 ; +\infty[ \) et décroissante sur \( ]-\infty ; 0[ \)

Question 6

La forme simplifiée de \( e^x \cdot e^{2x} \) est :

• a) \( e^{x^2 + 2x} \)
• b) \( e^{3x} \)
• c) \( e^{x} + e^{2x} \)
• d) \( 3e^{x} \)

Question 7

Le taux d'accroissement de \( f(x) = x^3 \) entre \( x = 1 \) et \( x = 2 \) est :

• a) 7
• b) 9
• c) 8
• d) 5

Question 8

La fonction \( f(x) = \cos(x) \) est :

• a) Paire
• b) Impaire
• c) Ni paire ni impaire
• d) Périodique mais pas paire

Question 9

La fonction \( f(x) = -x^2 + 2x \) admet un maximum en :

• a) \( x = -1 \)
• b) \( x = 0 \)
• c) \( x = 1 \)
• d) \( x = 2 \)

Question 10

La fonction \( f(x) = \sin(x) + \sin(x + 2\pi) \) est équivalente à :

• a) \( 2\sin(x) \)
• b) \( \sin(2x) \)
• c) \( 0 \)
• d) \( \sin(x) \)

Question 11

Les courbes de \( f(x) = x^2 \) et \( g(x) = 4x - 3 \) se coupent en :

• a) \( x = -1 \) et \( x = 4 \)
• b) \( x = 1 \) et \( x = 3 \)
• c) \( x = 0 \) et \( x = 4 \)
• d) \( x = 2 \) et \( x = 3 \)

Question 12

La dérivée de \( f(x) = e^{\sin(x)} \) est :

• a) \( \cos(x) \cdot e^{\sin(x)} \)
• b) \( \sin(x) \cdot e^{x} \)
• c) \( e^{\sin(x)} \cdot \sin(x) \)
• d) \( e^{\sin(x)} + \cos(x) \)

Soit la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = x^3 - 3x^2 + 4 \).

1. Comportement global
   1. Étudier le comportement de \( f \) quand \( x \) tend vers \( -\infty \) et \( +\infty \).
   2. Analyser le comportement local autour de \( x = 1 \) en calculant \( f(0.9) \), \( f(1) \) et \( f(1.1) \).
   3. Vérifier si \( f \) présente une symétrie particulière.
2. Analyse des variations
   1. Calculer \( f'(x) \) et étudier son signe.
   2. Déterminer les points où la dérivée s'annule sans changer de signe.
   3. Dresser le tableau de variations complet.
3. Tangentes particulières
   1. Déterminer l'équation de la tangente en \( x = 0 \).
   2. Trouver les points où la tangente est parallèle à \( y = -3x \).
   3. Étudier la position relative de la courbe par rapport à sa tangente en \( x = 2 \).

Soit la fonction \( g \) définie sur \( \mathbb{R}\setminus\{-1,1\} \) par \( g(x) = \frac{x^2 - 2x + 1}{x^2 - 1} \).

1. Étude locale
   1. Analyser le comportement autour de \( x = 1 \) en calculant \( g(0.9) \), \( g(1.1) \).
   2. Étudier le comportement au voisinage de \( x = -1 \).
   3. Calculer \( g(0) \), \( g(2) \) et \( g(-2) \).
2. Dérivation et extremums
   1. Simplifier l'expression de \( g(x) \) (factorisation possible).
   2. Calculer \( g'(x) \) et déterminer les points critiques.
   3. Étudier les variations sur chaque intervalle du domaine.
3. Propriétés géométriques
   1. Déterminer les points à tangente horizontale.
   2. Trouver l'équation de la tangente en \( x = 0 \).
   3. Montrer que \( (0,-1) \) est centre de symétrie.
4. Compléments
   1. Déterminer les intersections avec les axes.
   2. Résoudre \( g(x) = 0.5 \) et interpréter graphiquement.

Question 1

La dérivée de la fonction \( f(x) = 3e^{2x} \) est :

• a) \( 6e^{2x} \)
• b) \( 2e^{2x} \)
• c) \( 3e^{x} \)
• d) \( 6xe^{2x} \)

Question 2

La dérivée de la fonction \( f(x) = \sin(x)\cos(x) \) est :

• a) \( \cos^2(x) + \sin^2(x) \)
• b) \( \cos(x) - \sin(x) \)
• c) \( \cos(2x) \)
• d) \( \cos(x)^2 - \sin(x)^2 \)

Question 3

L'équation de la tangente à \( f(x) = e^x \) au point \( x = 1 \) est :

• a) \( y = e(x - 1) + e \)
• b) \( y = e^x \)
• c) \( y = ex + 1 \)
• d) \( y = e(x + 1) \)

Question 4

La fonction \( f(x) = \sin(x) \) est :

• a) Paire
• b) Impaire
• c) Ni paire ni impaire
• d) Constante

Question 5

La fonction \( f(x) = \tan(x) \) est définie sur :

• a) \( \mathbb{R} \setminus \{k\pi\} \)
• b) \( \mathbb{R} \setminus \{ \frac{\pi}{2} + k\pi \} \)
• c) \( \mathbb{R} \)
• d) \( ]-\frac{\pi}{2} ; \frac{\pi}{2}[ \)

Question 6

Les courbes de \( f(x) = x \) et \( g(x) = e^x \) se croisent en :

• a) \( x = 0 \)
• b) \( x = 1 \)
• c) Une seule fois pour \( x > 0 \)
• d) Jamais

Question 7

La fonction \( f(x) = e^{-x} \) est :

• a) Croissante
• b) Décroissante
• c) Constante
• d) Périodique

Question 8

La dérivée de \( f(x) = \tan(x) \) est :

• a) \( \sec^2(x) \)
• b) \( \cos^2(x) \)
• c) \( \tan(x)\cos(x) \)
• d) \( \frac{1}{\sin^2(x)} \)

Question 9

Le taux d'accroissement de \( f(x) = e^x \) entre \( x = 0 \) et \( x = 1 \) est :

• a) \( e \)
• b) \( e - 1 \)
• c) \( \frac{e - 1}{2} \)
• d) \( 1 \)

Question 10

La fonction \( f(x) = \cos(x) \) est périodique de période :

• a) \( \pi \)
• b) \( 2\pi \)
• c) \( \frac{\pi}{2} \)
• d) \( 4\pi \)

Question 11

Sur \( \mathbb{R} \), la fonction \( f(x) = e^x \) est :

• a) Strictement croissante
• b) Strictement décroissante
• c) Constante
• d) Périodique

Question 12

La fonction \( f(x) = \cos(x) \) est :

• a) Paire et périodique
• b) Impaire et périodique
• c) Ni paire ni impaire
• d) Paire mais non périodique

Soit la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = 3x^3 - 5x^2 + 2 \).

1. Comportement global et local
   1. Analyser le comportement de \( f \) en \( ±\infty \) par calcul direct
   2. Étudier localement autour de x=1 en calculant \(f(0.9)\), \(f(1)\) et \(f(1.1)\)
   3. Vérifier si la fonction admet des symétries
2. Dérivation et points critiques
   1. Calculer f'(x) et déterminer les points critiques
   2. Étudier le signe de la dérivée première
   3. Dresser le tableau de variations complet
3. Étude des tangentes
   1. Déterminer l'équation de la tangente en x=0
   2. Trouver les points où la tangente est parallèle à y=4x
   3. Étudier la position relative courbe/tangente en x=1

Soit la fonction \( g \) définie sur \( \mathbb{R}\setminus\{2\} \) par \( g(x) = \frac{2x^2 - 3x + 1}{x - 2} \).

1. Analyse locale
   1. Étudier le comportement autour de x=2 par calcul de g(1.9) et g(2.1)
   2. Calculer g(0), g(1) et g(3)
   3. Vérifier la parité de la fonction
2. Dérivation et variations
   1. Calculer g'(x) sous forme simplifiée
   2. Déterminer les extremums locaux
   3. Établir le tableau de variations
3. Propriétés géométriques
   1. Trouver les points à tangente horizontale
   2. Déterminer l'équation de la tangente en x=1
   3. Rechercher d'éventuels centres de symétrie
4. Problèmes complémentaires
   1. Déterminer les intersections avec les axes
   2. Résoudre g(x)=3 et interpréter graphiquement

Question 1

La dérivée de \( f(x) = \frac{x^2 + 1}{x} \) est :

• a) \( \frac{2x \cdot x - (x^2 + 1)}{x^2} \)
• b) \( \frac{2x - \frac{x^2 + 1}{x^2}}{x^2} \)
• c) \( \frac{x^2 - 1}{x^2} \)
• d) \( \frac{x^2 - 1}{x} \)

Question 2

L'équation de la tangente à la courbe de \( f(x) = \sqrt{x} \) au point \( x = 4 \) est :

• a) \( y = \frac{1}{4}(x - 4) + 2 \)
• b) \( y = \frac{1}{4}x + 2 \)
• c) \( y = \frac{1}{2}(x - 4) + 2 \)
• d) \( y = \frac{1}{2}x - 2 \)

Question 3

Le domaine de définition de \( f(x) = \sqrt{x - 2} \) est :

• a) \( ]-\infty ; 2[ \)
• b) \( [2 ; +\infty[ \)
• c) \( ]2 ; +\infty[ \)
• d) \( \mathbb{R} \)

Question 4

Si \( f'(a) = 0 \) et que \( f''(a) > 0 \), alors :

• a) \( f \) est croissante en \( a \)
• b) \( f \) a un minimum local en \( a \)
• c) \( f \) a un maximum local en \( a \)
• d) \( f \) est décroissante en \( a \)

Question 5

La courbe de la fonction \( f(x) = 3x^2 - 2x + 1 \) coupe l'axe des ordonnées en :

• a) \( y = 1 \)
• b) \( y = 0 \)
• c) \( y = -2 \)
• d) \( y = 3 \)

Question 6

La pente de la tangente à \( f(x) = x^3 \) au point \( x = 2 \) est :

• a) 3
• b) 6
• c) 12
• d) 4

Question 7

Le taux d'accroissement de \( f(x) = x^2 - 1 \) entre \( x = 1 \) et \( x = 3 \) est :

• a) 2
• b) 3
• c) 4
• d) 5

Question 8

La fonction \( f(x) = x^5 - x \) est :

• a) Paire
• b) Impaire
• c) Ni paire ni impaire
• d) Périodique

Question 9

La courbe de \( f(x) = (x + 3)^2 \) est symétrique par rapport à :

• a) L’axe des abscisses
• b) La droite \( x = 0 \)
• c) La droite \( x = -3 \)
• d) La droite \( y = x \)

Question 10

Si \( f'(x) = (x-1)(x+2) \), alors \( f \) est :

• a) Croissante sur \( ]-\infty ; -2[ \) et \( ]1 ; +\infty[ \)
• b) Décroissante sur \( ]-\infty ; -2[ \cup ]1 ; +\infty[ \)
• c) Maximum local en \( x = -2 \)
• d) Minimum local en \( x = 1 \)

Question 11

Les courbes de \( f(x) = x^2 \) et \( g(x) = 4 - x \) se croisent en :

• a) \( x = 2 \)
• b) \( x = -1 \) et \( x = 4 \)
• c) \( x = 1 \) et \( x = 2 \)
• d) \( x = -2 \) et \( x = 2 \)

Question 12

Si la dérivée \( f'(x) > 0 \) pour tout \( x \in \mathbb{R} \), alors :

• a) \( f \) est décroissante
• b) \( f \) est constante
• c) \( f \) est croissante
• d) \( f \) est paire

Soit la fonction \( f \) définie sur \( \mathbb{R} \) par \( f(x) = -x^2 + 4x \).

1. Étude de base
   1. Déterminer les intersections de \( \mathcal{C}_f \) avec l'axe des abscisses.
   2. Calculer les coordonnées du sommet de la parabole.
   3. Tracer l'allure de la courbe en annotant ces éléments.
2. Calcul d'aire
   1. Déterminer l'équation de la tangente \( T \) au point d'abscisse \( x = 1 \).
   2. Calculer l'aire du triangle formé par \( T \) et les axes du repère.
   3. Déterminer l'aire de la région délimitée par \( \mathcal{C}_f \), l'axe des abscisses et les droites \( x = 0 \), \( x = 4 \).
3. Problème géométrique
   1. Montrer que la droite \( y = x \) coupe \( \mathcal{C}_f \) en deux points.
   2. Calculer l'aire du domaine compris entre ces deux courbes.

Soit la fonction \( g \) définie sur \( \mathbb{R}\setminus\{-1\} \) par \( g(x) = \frac{2x^2 - x - 1}{x + 1} \).

1. Analyse préliminaire
   1. Simplifier l'expression de \( g(x) \) pour \( x \neq -1 \).
   2. Calculer \( g(-2) \), \( g(0) \) et \( g(1) \).
   3. Étudier la parité de \( g \).
2. Dérivation et variations
   1. Calculer \( g'(x) \) et étudier son signe.
   2. Dresser le tableau de variations complet.
   3. Déterminer les extremums locaux.
3. Tangentes et symétrie
   1. Déterminer l'équation de la tangente en \( x = 0 \).
   2. Trouver les points où la tangente est horizontale.
   3. Montrer que \( \mathcal{C}_g \) admet un centre de symétrie.

Barème indicatif :

• QCM : 0,5 point par question (6 points)
• Exercice 1 : 7 points
• Exercice 2 : 7 points