Cours

📔 Fonctions trigonométriques

Etude des fonctions trigonométriques

1. Repérage sur le cercle trigonométrique

Le cercle trigonométrique est un outil fondamental pour comprendre les fonctions trigonométriques. Il s'agit d'un cercle de rayon 1 centré à l'origine (0,0) du plan cartésien. Cette construction géométrique permet de visualiser concrètement la relation entre les angles et les valeurs trigonométriques correspondantes.

L'utilisation du rayon unité n'est pas anodine : elle simplifie considérablement les calculs et permet une correspondance directe entre la mesure d'un angle en radians et la longueur de l'arc correspondant sur le cercle. Cette propriété fondamentale fait du radian une unité naturelle pour mesurer les angles.

Caractéristiques clés

Rayon unité : Le rayon vaut toujours 1, ce qui permet d'identifier directement cos(θ) et sin(θ) aux coordonnées cartésiennes
Sens positif : Anti-horaire (sens inverse des aiguilles d'une montre), convention universelle en mathématiques
Angles remarquables : 0, \(\frac{\pi}{6}\), \(\frac{\pi}{4}\), \(\frac{\pi}{3}\), \(\frac{\pi}{2}\) radians qui correspondent à des valeurs trigonométriques "simples"
Quadrants : Le plan est divisé en 4 quadrants qui déterminent les signes des coordonnées et donc des fonctions trigonométriques
Périodicité : Un tour complet correspond à \(2\pi\) radians, ce qui explique la périodicité des fonctions trigonométriques

L'orientation positive (sens trigonométrique) est cruciale pour définir correctement les angles orientés. Cette convention permet de distinguer les rotations dans un sens ou dans l'autre, donnant ainsi une signification algébrique aux angles.

Figure 1 : Cercle trigonométrique avec point M et ses projections orthogonales

2. Coordonnées d'un point du cercle trigonométrique

Définition fondamentale

Pour tout angle θ (en radians), le point M correspondant sur le cercle trigonométrique a pour coordonnées cartésiennes le couple formé par le cosinus et le sinus de cet angle. Cette définition géométrique est à la base de toute la trigonométrie.

\[ M(\theta) = (\cos(\theta), \sin(\theta)) \]

Cette relation fondamentale permet de définir géométriquement les fonctions cosinus et sinus. L'abscisse du point M correspond au cosinus de l'angle θ, tandis que l'ordonnée correspond au sinus de θ. Cette interprétation géométrique rend intuitive la compréhension des propriétés trigonométriques.

Il est important de noter que cette définition s'étend naturellement à tous les angles réels, même ceux supérieurs à \(2\pi\) ou négatifs, grâce à la périodicité du cercle.

Valeurs remarquables

Les angles remarquables correspondent à des positions particulières sur le cercle trigonométrique, pour lesquelles les valeurs trigonométriques s'expriment simplement à l'aide de radicaux. Ces valeurs sont essentielles à mémoriser car elles reviennent constamment dans les calculs.

θ (rad)	θ (°)	cos(θ)	sin(θ)
0	0°	1	0
\(\frac{\pi}{6}\)	30°	\(\frac{\sqrt{3}}{2}\)	\(\frac{1}{2}\)
\(\frac{\pi}{4}\)	45°	\(\frac{\sqrt{2}}{2}\)	\(\frac{\sqrt{2}}{2}\)
\(\frac{\pi}{3}\)	60°	\(\frac{1}{2}\)	\(\frac{\sqrt{3}}{2}\)
\(\frac{\pi}{2}\)	90°	0	1

Astuce mnémotechnique : Pour retenir ces valeurs, on peut utiliser la règle des "racines" : pour sin(0°, 30°, 45°, 60°, 90°), on a \(\frac{\sqrt{0}}{2}\), \(\frac{\sqrt{1}}{2}\), \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{3}}{2}\), \(\frac{\sqrt{4}}{2}\). Pour le cosinus, c'est l'inverse.

Visualisation des angles remarquables

Figure 2 : Positionnement des angles remarquables sur le cercle trigonométrique

Exemple détaillé

Considérons l'angle θ = \(\frac{\pi}{4}\) (45°) :

\[ M\left(\frac{\pi}{4}\right) = \left(\cos\left(\frac{\pi}{4}\right), \sin\left(\frac{\pi}{4}\right)\right) = \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2}\right) \]

Ce point se situe exactement à mi-chemin entre les axes x et y dans le premier quadrant. La symétrie de cette position explique pourquoi cosinus et sinus ont la même valeur pour cet angle particulier.

Cette égalité \(\cos\left(\frac{\pi}{4}\right) = \sin\left(\frac{\pi}{4}\right)\) illustre parfaitement la complémentarité entre ces deux fonctions trigonométriques.

3. Fonction cosinus

Définition et propriétés

La fonction cosinus, notée cos, associe à tout angle θ l'abscisse du point correspondant sur le cercle trigonométrique. Cette fonction est fondamentale en trigonométrie et possède des propriétés remarquables qui la rendent indispensable dans de nombreux domaines des mathématiques et de la physique.

\[ \cos: \mathbb{R} \rightarrow [-1, 1] \] \[ \theta \mapsto \cos(\theta) \]

Propriétés principales :

Période : \(2\pi\) (cos(θ + 2π) = cos(θ)), ce qui signifie que la fonction se répète identiquement tous les \(2\pi\) radians
Parité : fonction paire (cos(-θ) = cos(θ)), la courbe est symétrique par rapport à l'axe des ordonnées
Maximum : 1 atteint en θ = 2kπ (k ∈ ℤ), correspondant aux positions "est" du cercle
Minimum : -1 atteint en θ = π + 2kπ (k ∈ ℤ), correspondant aux positions "ouest" du cercle
Continuité : La fonction cosinus est continue sur tout ℝ
Dérivabilité : La fonction cosinus est dérivable sur tout ℝ avec cos'(θ) = -sin(θ)

Applications et formules importantes

La fonction cosinus intervient dans de nombreuses formules trigonométriques fondamentales :

Identité pythagoricienne : \(\cos^2(\theta) + \sin^2(\theta) = 1\)

Formules d'addition :
\(\cos(a + b) = \cos(a)\cos(b) - \sin(a)\sin(b)\)
\(\cos(a - b) = \cos(a)\cos(b) + \sin(a)\sin(b)\)

Ces formules sont essentielles pour résoudre des équations trigonométriques complexes et pour simplifier des expressions.

4. Fonction sinus

Définition et propriétés

La fonction sinus, notée sin, associe à tout angle θ l'ordonnée du point correspondant sur le cercle trigonométrique. Complémentaire de la fonction cosinus, elle possède des propriétés similaires mais décalées, ce qui lui confère un rôle particulier dans la modélisation des phénomènes périodiques.

\[ \sin: \mathbb{R} \rightarrow [-1, 1] \] \[ \theta \mapsto \sin(\theta) \]

Propriétés principales :

Période : \(2\pi\) (sin(θ + 2π) = sin(θ)), même périodicité que le cosinus
Parité : fonction impaire (sin(-θ) = -sin(θ)), la courbe est symétrique par rapport à l'origine
Maximum : 1 atteint en θ = π/2 + 2kπ (k ∈ ℤ), correspondant aux positions "nord" du cercle
Minimum : -1 atteint en θ = 3π/2 + 2kπ (k ∈ ℤ), correspondant aux positions "sud" du cercle
Continuité : La fonction sinus est continue sur tout ℝ
Dérivabilité : La fonction sinus est dérivable sur tout ℝ avec sin'(θ) = cos(θ)

Relation avec le cosinus

Les fonctions sinus et cosinus sont intimement liées par plusieurs relations importantes :

Déphasage : \(\sin(\theta) = \cos\left(\frac{\pi}{2} - \theta\right)\)

Relation de complémentarité : \(\cos(\theta) = \sin\left(\frac{\pi}{2} - \theta\right)\)

Ces relations montrent que le sinus et le cosinus sont des fonctions "décalées" l'une par rapport à l'autre de π/2 radians (90°). Cette propriété est fondamentale pour comprendre les phénomènes vibratoires et ondulatoires.

Représentation graphique

Figure 4 : Représentation graphique de la fonction sinus sur [0, 2π]

Variations et signe

L'analyse des variations du sinus sur une période :

1er quadrant [0, π/2] : sin(θ) > 0 et croissant de 0 à 1
2ème quadrant [π/2, π] : sin(θ) > 0 et décroissant de 1 à 0
3ème quadrant [π, 3π/2] : sin(θ) < 0 et décroissant de 0 à -1
4ème quadrant [3π/2, 2π] : sin(θ) < 0 et croissant de -1 à 0

Le sinus est positif dans les quadrants I et II (partie supérieure du cercle) et négatif dans les quadrants III et IV (partie inférieure).

5. Relations et identités trigonométriques

Identités fondamentales

Les relations trigonométriques sont des égalités vérifiées pour toutes les valeurs de θ où elles sont définies. Elles constituent la base du calcul trigonométrique.

Identité pythagoricienne :
\(\cos^2(\theta) + \sin^2(\theta) = 1\)

Cette identité découle directement du théorème de Pythagore appliqué au triangle rectangle formé par les projections du point M sur les axes.

Formules de parité :
\(\cos(-\theta) = \cos(\theta)\) (fonction paire)
\(\sin(-\theta) = -\sin(\theta)\) (fonction impaire)

Formules de périodicité :
\(\cos(\theta + 2\pi) = \cos(\theta)\)
\(\sin(\theta + 2\pi) = \sin(\theta)\)

Formules d'addition

Ces formules permettent de calculer les valeurs trigonométriques d'une somme ou d'une différence d'angles :

Cosinus :
\(\cos(a + b) = \cos(a)\cos(b) - \sin(a)\sin(b)\)
\(\cos(a - b) = \cos(a)\cos(b) + \sin(a)\sin(b)\)

Sinus :
\(\sin(a + b) = \sin(a)\cos(b) + \cos(a)\sin(b)\)
\(\sin(a - b) = \sin(a)\cos(b) - \cos(a)\sin(b)\)

Ces formules sont essentielles pour résoudre des équations trigonométriques et pour effectuer des calculs dans des contextes géométriques complexes.

Superposition des courbes

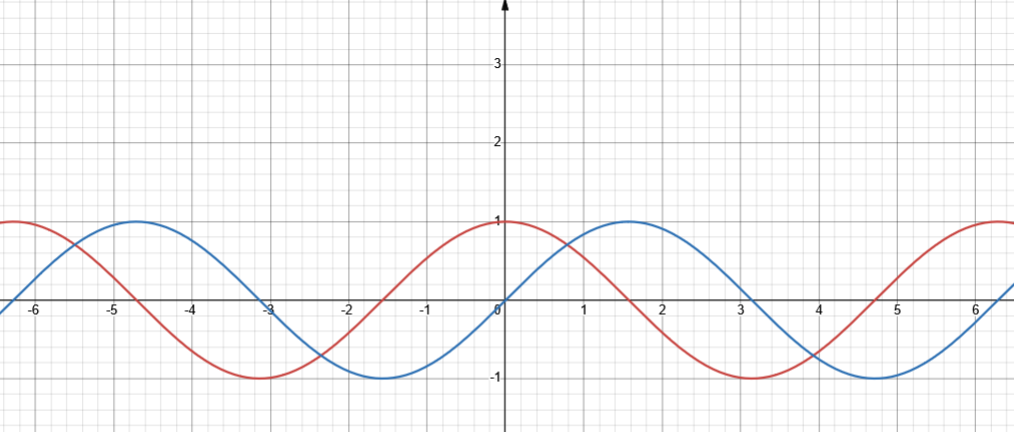
Figure 5 : Superposition des courbes cosinus et sinus montrant le déphasage de π/2

Formules de duplication

Ces formules permettent de calculer les valeurs trigonométriques d'un angle double :

\(\cos(2\theta) = \cos^2(\theta) - \sin^2(\theta)\)
\(\cos(2\theta) = 2\cos^2(\theta) - 1\)
\(\cos(2\theta) = 1 - 2\sin^2(\theta)\)

\(\sin(2\theta) = 2\sin(\theta)\cos(\theta)\)

Ces formules sont particulièrement utiles pour simplifier des expressions trigonométriques complexes et pour résoudre certains types d'équations.

6. Applications et exercices pratiques

Résolution d'équations trigonométriques

La résolution d'équations trigonométriques nécessite une bonne maîtrise du cercle trigonométrique et des valeurs remarquables. Voici quelques exemples typiques avec leur méthode de résolution.

Exemple 1 : Équation cosinus

Résoudre \(\cos(x) = \frac{1}{2}\) dans l'intervalle [0, 2π]

\[ x = \frac{\pi}{3} \quad \text{ou} \quad x = \frac{5\pi}{3} \]

Sur le cercle trigonométrique, ces solutions correspondent aux angles dont la projection horizontale vaut 1/2.

Exemple 2 : Équation sinus

Résoudre \(\sin(x) = -\frac{\sqrt{2}}{2}\) dans ℝ

\[ x = \frac{5\pi}{4} + 2k\pi \quad \text{ou} \quad x = \frac{7\pi}{4} + 2k\pi \quad (k \in \mathbb{Z}) \]

Ces solutions correspondent aux points du cercle où l'ordonnée vaut -√2/2, situés dans les 3ème et 4ème quadrants.

Applications physiques

Les fonctions trigonométriques modélisent de nombreux phénomènes périodiques en physique et en ingénierie :

Mouvement harmonique : \(x(t) = A\cos(\omega t + \phi)\) décrit les oscillations
Ondes : \(y(x,t) = A\sin(kx - \omega t)\) modélise une onde progressive
Courant alternatif : \(I(t) = I_0\sin(2\pi ft)\) représente un signal électrique
Mécanique céleste : Position des planètes sur leur orbite

Ces applications montrent l'importance de maîtriser les concepts trigonométriques pour comprendre de nombreux phénomènes naturels et technologiques.

Exercices guidés

Exercice 1 : Calcul de valeurs exactes

Calculer les valeurs exactes de :

\(\cos\left(\frac{7\pi}{6}\right)\)
\(\sin\left(\frac{3\pi}{4}\right)\)
\(\tan\left(\frac{5\pi}{3}\right)\)

Indice : Utiliser les symétries du cercle trigonométrique et les valeurs remarquables.

Exercice 2 : Résolution d'équations

Résoudre dans [0, 2π] :

\(2\cos(x) + 1 = 0\)
\(\sin(x) = \cos(x)\)
\(\cos^2(x) - \frac{3}{4} = 0\)

Méthode : Isoler la fonction trigonométrique puis utiliser le cercle unité.

Exercice 3 : Problème concret

La hauteur des marées dans un port suit approximativement la fonction :

\[ h(t) = 3 + 2\cos\left(\frac{\pi}{6}t\right) \]

où t est le temps en heures depuis minuit.

Quelle est la hauteur maximale de la marée ?
À quels moments la marée est-elle à son niveau moyen ?

Conseils méthodologiques

Visualisation : Dessiner systématiquement le cercle trigonométrique pour localiser les solutions
Périodicité : N'oubliez pas d'ajouter \(2k\pi\) pour les solutions générales
Symétries : Exploiter les relations comme \(\cos(\pi - x) = -\cos(x)\)
Vérification : Toujours remplacer les solutions dans l'équation originale
Unités : Attention à travailler en radians ou en degrés selon le contexte

📐 Simulateur Trigonométrique Interactif

⚙️ Contrôles

Angle θ (degrés):

0° 30° 360°

📚 Formules Fondamentales

sin θ = y/r (ordonnée/rayon)

cos θ = x/r (abscisse/rayon)

tan θ = y/x = sin θ/cos θ

sin²θ + cos²θ = 1 (identité fondamentale)

🔢 Valeurs Calculées

sin θ: 0.500

cos θ: 0.866

tan θ: 0.577

θ (rad): 0.524

🎯 Cercle Trigonométrique

📈 Graphiques des Fonctions Trigonométriques

Exercice 1: ★ ★ ★ ☆ ☆

Calculez \( \sin\left(\frac{\pi}{6}\right) \) et \( \cos\left(\frac{\pi}{6}\right) \).

Pour calculer \( \sin\left(\frac{\pi}{6}\right) \) et \( \cos\left(\frac{\pi}{6}\right) \) :

Utiliser les valeurs connues : Nous savons que \( \sin\left(\frac{\pi}{6}\right) = \frac{1}{2} \) et \( \cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2} \).

Ainsi, \( \sin\left(\frac{\pi}{6}\right) = \frac{1}{2} \) et \( \cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2} \).

Exercice 2: ★ ★ ★ ★ ☆

Déterminez la valeur de \( \tan\left(\frac{\pi}{4}\right) \).

Pour calculer \( \tan\left(\frac{\pi}{4}\right) \) :

Utiliser la définition : Nous savons que \( \tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)} \).
Calculer : Pour \( \theta = \frac{\pi}{4} \), \( \sin\left(\frac{\pi}{4}\right) = \cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2} \). Donc, \( \tan\left(\frac{\pi}{4}\right) = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = 1 \).

Ainsi, \( \tan\left(\frac{\pi}{4}\right) = 1 \).

Exercice 3: ★ ★ ★ ★ ★

Calculez \( \sin(30^\circ) \) et \( \cos(30^\circ) \) en utilisant le cercle trigonométrique.

Pour calculer \( \sin(30^\circ) \) et \( \cos(30^\circ) \) :

Utiliser les valeurs connues : Nous savons que \( \sin(30^\circ) = \frac{1}{2} \) et \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \).

Ainsi, \( \sin(30^\circ) = \frac{1}{2} \) et \( \cos(30^\circ) = \frac{\sqrt{3}}{2} \).

Exercice 4: ★ ★ ★ ☆ ☆

Calculez la valeur de \( \sin(90^\circ) \) et \( \cos(90^\circ) \).

Pour calculer \( \sin(90^\circ) \) et \( \cos(90^\circ) \) :

Utiliser les valeurs connues : Nous savons que \( \sin(90^\circ) = 1 \) et \( \cos(90^\circ) = 0 \).

Ainsi, \( \sin(90^\circ) = 1 \) et \( \cos(90^\circ) = 0 \).

Exercice 5: ★ ★ ★ ★ ☆

Évaluez \( \sin(45^\circ) \) et \( \cos(45^\circ) \) en utilisant le cercle trigonométrique.

Pour évaluer \( \sin(45^\circ) \) et \( \cos(45^\circ) \) :

Utiliser les valeurs connues : Nous savons que \( \sin(45^\circ) = \cos(45^\circ) = \frac{\sqrt{2}}{2} \).

Ainsi, \( \sin(45^\circ) = \frac{\sqrt{2}}{2} \) et \( \cos(45^\circ) = \frac{\sqrt{2}}{2} \).

Exercice 6: ★ ★ ★ ★ ☆

Déterminez le domaine de la fonction \( f(x) = \cos(x) \).

Le domaine de la fonction \( f(x) = \cos(x) \) est l'ensemble des réels \( \mathbb{R} \) car la fonction cosinus est définie pour tous les nombres réels.

Exercice 7: ★ ★ ★ ★ ★

Quelle est la période de la fonction \( f(x) = \sin(x) \) ?

La période de la fonction \( f(x) = \sin(x) \) est \( 2\pi \). Cela signifie que pour tout \( x \), \( \sin(x + 2\pi) = \sin(x) \).

Exercice 8: ★ ★ ★ ☆ ☆

Calculez la dérivée de la fonction \( f(x) = \sin(x) \) et interprétez le résultat.

La dérivée de la fonction \( f(x) = \sin(x) \) est :

\( f'(x) = \cos(x) \).

Cela signifie que la pente de la courbe de \( \sin(x) \) à un point donné est égale à la valeur de \( \cos(x) \) à ce point.

Exercice 9: ★ ★ ★ ★ ☆

Étudiez les variations de la fonction \( f(x) = \cos(x) \) sur l'intervalle \( [0, 2\pi] \).

Pour étudier les variations de \( f(x) = \cos(x) \) sur \( [0, 2\pi] \) :

La dérivée est \( f'(x) = -\sin(x) \).
Les points critiques sont \( x = 0, \pi, 2\pi \).
Sur \( [0, \pi] \), \( f \) est décroissante. Sur \( [\pi, 2\pi] \), \( f \) est croissante.

Ainsi, \( f(x) \) atteint un maximum à \( x = 0 \) et un minimum à \( x = \pi \).

Exercice 10: ★ ★ ★ ★ ★

Tracez les courbes des fonctions \( f(x) = \sin(x) \) et \( g(x) = \cos(x) \) sur l'intervalle \( [-2\pi, 2\pi] \) et commentez les résultats.

Pour tracer les courbes :

Les deux fonctions oscillent entre -1 et 1.
La fonction \( \sin(x) \) passe par l'origine, tandis que \( \cos(x) \) commence à 1.
Les périodicités des deux fonctions sont \( 2\pi \).

Les courbes montrent que \( \sin(x) \) et \( \cos(x) \) sont décalées de \( \frac{\pi}{2} \) l'une par rapport à l'autre.

Figure 1 : Courbes des fonctions sinus (bleu) et cosinus (rouge) sur l'intervalle \( [-2\pi, 2\pi] \)

Forum(s) associé(s)

Page:

📔 Fonctions trigonométriques

1. Repérage sur le cercle trigonométrique

Caractéristiques clés

2. Coordonnées d'un point du cercle trigonométrique

Définition fondamentale

Valeurs remarquables

Visualisation des angles remarquables

Exemple détaillé

3. Fonction cosinus

Définition et propriétés

Applications et formules importantes

4. Fonction sinus

Définition et propriétés

Relation avec le cosinus

Représentation graphique

Variations et signe

5. Relations et identités trigonométriques

Identités fondamentales

Formules d'addition

Superposition des courbes

Formules de duplication

6. Applications et exercices pratiques

Résolution d'équations trigonométriques

Exemple 1 : Équation cosinus

Exemple 2 : Équation sinus

Applications physiques

Exercices guidés

Exercice 1 : Calcul de valeurs exactes

Exercice 2 : Résolution d'équations

Exercice 3 : Problème concret

Conseils méthodologiques

📐 Simulateur Trigonométrique Interactif

⚙️ Contrôles

📚 Formules Fondamentales

🔢 Valeurs Calculées

🎯 Cercle Trigonométrique

📈 Graphiques des Fonctions Trigonométriques

Exercice 1: ★ ★ ★ ☆ ☆

Exercice 2: ★ ★ ★ ★ ☆

Exercice 3: ★ ★ ★ ★ ★

Exercice 4: ★ ★ ★ ☆ ☆

Exercice 5: ★ ★ ★ ★ ☆

Exercice 6: ★ ★ ★ ★ ☆

Exercice 7: ★ ★ ★ ★ ★

Exercice 8: ★ ★ ★ ☆ ☆

Exercice 9: ★ ★ ★ ★ ☆

Exercice 10: ★ ★ ★ ★ ★

Forum(s) associé(s)

Articles exclusifs

Ateliers Pratiques

Ateliers en Informatique

Ateliers en Mathématiques

Ateliers de Développement Personnel

Ateliers en Sciences Appliquées

Tags

Nos cours

Liens

Support