madamasterclass.com
Analyse des notions de graphes dans les réseaux.
Les graphes sont des structures mathématiques essentielles qui modélisent des relations entre différents objets. Dans le contexte des réseaux, les graphes permettent de représenter les connexions entre utilisateurs, informations et ressources, facilitant ainsi l'analyse des interactions et des flux d'information.
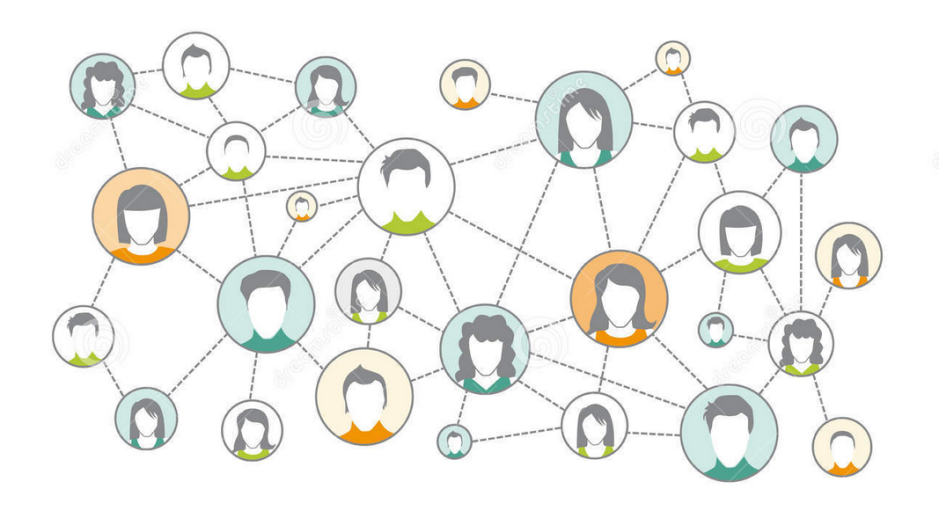
Un graphe est composé de nœuds (ou sommets) et d'arêtes (ou liens) qui relient ces nœuds. Les nœuds représentent des entités (utilisateurs, pages, etc.), tandis que les arêtes représentent les connexions ou relations entre ces entités.
Les graphes sont utilisés dans divers domaines pour analyser et optimiser les réseaux :
La compréhension des notions de graphes est fondamentale pour analyser les réseaux modernes. En utilisant des graphes pour modéliser les relations, on peut mieux appréhender les dynamiques sociales, les flux d'information et optimiser les interactions au sein des réseaux.
Ce cours présente les termes clés liés aux graphes, essentiels pour comprendre leur structure et leur utilisation dans divers domaines.
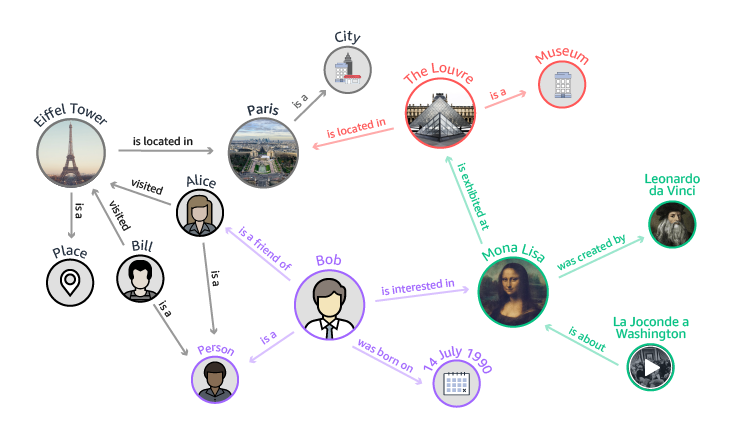
Un nœud, ou sommet, est une entité dans un graphe qui représente un objet ou un point d'intérêt. Par exemple, dans un réseau social, chaque utilisateur peut être considéré comme un nœud.
Une arête est une connexion entre deux nœuds dans un graphe. Elle peut être orientée (indiquant une direction) ou non orientée. Dans un réseau social, une arête peut représenter une relation d'amitié ou de suivi.
Un graphe orienté est un type de graphe où les arêtes ont une direction, indiquant une relation asymétrique. Par exemple, dans un réseau de suivis, une arête peut aller d'un utilisateur A à un utilisateur B, signifiant que A suit B, mais pas nécessairement l'inverse.
Un graphe non orienté est un graphe où les arêtes n'ont pas de direction. Cela signifie que la relation entre les nœuds est symétrique, comme dans le cas d'une amitié où A est ami avec B et vice versa.
Le degré d'un nœud est le nombre d'arêtes qui lui sont connectées. Dans un réseau social, cela peut représenter le nombre d'amis ou de connexions qu'un utilisateur a.
Une composante connexe est un sous-ensemble de nœuds dans un graphe où chaque paire de nœuds est connectée par un chemin. Les nœuds d'une même composante sont accessibles les uns des autres.
Un graphe pondéré attribue des poids aux arêtes, représentant la force ou le coût de la connexion. Par exemple, dans un réseau de transport, le poids d'une arête peut représenter la distance ou le temps nécessaire pour voyager entre deux nœuds.
Un chemin est une séquence de nœuds reliés par des arêtes. Il peut être utilisé pour représenter un itinéraire dans un réseau, indiquant comment passer d'un nœud à un autre.
Un cycle est un chemin qui commence et se termine au même nœud, sans passer deux fois par le même nœud. Les cycles sont importants pour détecter les boucles dans les réseaux.
Un graphe complet est un graphe où chaque paire de nœuds est connectée par une arête. Dans un réseau, cela représente une situation où tous les nœuds sont directement interconnectés.
Un graphe est une structure mathématique fondamentale qui permet de modéliser des relations entre objets. Il est composé d'un ensemble fini de sommets (ou nœuds) reliés par des arêtes. Cette représentation abstraite capture l'essence de nombreux phénomènes réels où les connexions entre entités sont plus importantes que les entités elles-mêmes.
Formellement, un graphe G est défini par le couple \(G = (V, E)\) où V est l'ensemble des sommets et E l'ensemble des arêtes. Cette simplicité conceptuelle cache une richesse extraordinaire d'applications, de la modélisation des réseaux sociaux à l'optimisation des circuits électroniques.
Figure 1 : Graphe simple avec 6 sommets et 6 arêtes
Figure 2 : Différents types de graphes
Pour un graphe G = (V, E) avec |V| = n, la matrice d'adjacence A est une matrice n × n où :
\(A_{ij} = \begin{cases} 1 & \text{si } (v_i, v_j) \in E \\ 0 & \text{sinon} \end{cases}\)
Exemple pour le graphe de la Figure 1 :
Éducation
A = [[0, 1, 0, 1, 1, 0],
[1, 0, 1, 0, 1, 0],
[0, 1, 0, 0, 0, 1],
[1, 0, 0, 0, 0, 0],
[1, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0]]
Propriétés :
Chaque sommet maintient une liste de ses voisins. Plus efficace pour les graphes creux.
adj_list = {
'A': ['B', 'D', 'E'],
'B': ['A', 'C', 'E'],
'C': ['B', 'F'],
'D': ['A'],
'E': ['A', 'B'],
'F': ['C']
}
Complexités :
| Critère | Matrice | Liste |
|---|---|---|
| Espace mémoire | O(|V|²) | O(|V|+|E|) |
| Test d'adjacence | O(1) | O(deg(v)) |
| Parcours voisins | O(|V|) | O(deg(v)) |
| Ajout/suppression | O(1) | O(deg(v)) |
| Graphes creux | Inefficace | Optimal |
Choix pratique : Utilisez les listes d'adjacence pour les graphes réels (souvent creux) et les matrices pour les calculs théoriques ou les graphes denses.
Explore en profondeur avant d'explorer en largeur. Utilise une pile (ou la récursion).
Algorithme :
DFS(G, s):
marquer s comme visité
pour chaque voisin v de s:
si v non visité:
DFS(G, v)
Complexité : O(|V| + |E|)
Applications : Détection de cycles, tri topologique, composantes connexes
Explore niveau par niveau. Utilise une file (FIFO).
Algorithme :
BFS(G, s):
file = [s]
marquer s comme visité
tant que file non vide:
u = file.pop()
pour chaque voisin v de u:
si v non visité:
marquer v comme visité
file.append(v)
Complexité : O(|V| + |E|)
Applications : Plus court chemin non pondéré, arbre couvrant, test de bipartition
Figure 3 : Parcours BFS - exploration niveau par niveau
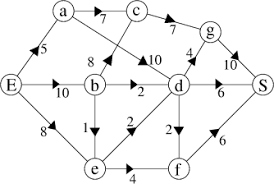
Formule de relaxation (Dijkstra) :
\(d[v] = \min(d[v], d[u] + w(u,v))\)
Mesure la plus simple : nombre de connexions directes d'un sommet.
\(C_D(v) = \deg(v) = |\{u : (u,v) \in E\}|\)
Version normalisée : \(C_D'(v) = \frac{\deg(v)}{n-1}\)
Interprétation : Un sommet central par degré a de nombreuses connexions directes, ce qui peut indiquer une influence locale importante.
Mesure la facilité d'atteindre tous les autres sommets.
\(C_C(v) = \frac{1}{\sum_{u \in V} d(v,u)}\)
où \(d(v,u)\) est la distance géodésique entre v et u.
Interprétation : Un sommet central par proximité peut rapidement atteindre tous les autres sommets.
Mesure le rôle de "pont" d'un sommet dans les communications.
\(C_B(v) = \sum_{s \neq v \neq t} \frac{\sigma_{st}(v)}{\sigma_{st}}\)
où \(\sigma_{st}\) est le nombre de plus courts chemins entre s et t, et \(\sigma_{st}(v)\) le nombre passant par v.
Interprétation : Un sommet avec une forte centralité d'intermédiarité contrôle les flux d'information.
Un sommet est central s'il est connecté à des sommets eux-mêmes centraux.
\(C_E(v) = \frac{1}{\lambda} \sum_{u \in N(v)} C_E(u)\)
où λ est la plus grande valeur propre et N(v) les voisins de v.
Application célèbre : PageRank de Google utilise cette idée pour classer les pages web.
Figure 4 : Analyse de centralité - A est le sommet le plus central selon tous les critères
Trouver l'arbre de poids minimal qui connecte tous les sommets.
Algorithme de Kruskal : Trier les arêtes et les ajouter sans créer de cycle.
Algorithme de Prim : Construire l'arbre sommet par sommet.
Complexité : O(|E| log |E|) pour les deux algorithmes.
Application : Réseaux de communication, distribution électrique.
Maximiser le débit d'un réseau avec des contraintes de capacité.
Théorème fondamental : Le flot maximal égale la coupe minimale.
\(\max \text{-flot} = \min \text{-coupe}\)
Algorithmes : Ford-Fulkerson, Edmonds-Karp, push-relabel.
Applications : Transport, réseaux informatiques, appariement.
Plusieurs problèmes sur les graphes sont NP-complets :
Approches : Heuristiques, approximation, programmation dynamique.
Attribuer des couleurs aux sommets tels que deux sommets adjacents aient des couleurs différentes.
Nombre chromatique χ(G) : minimum de couleurs nécessaires.
Borne supérieure : \(\chi(G) \leq \Delta(G) + 1\) où Δ(G) est le degré maximal.
Algorithme glouton : Colorier les sommets dans l'ordre, en choisissant la plus petite couleur possible.
Applications : Planification d'examens, allocation de ressources.
Trouver un ensemble d'arêtes sans sommet commun.
Appariement parfait : Chaque sommet est incident à exactement une arête de l'appariement.
Théorème de König : Dans un graphe biparti, la taille de l'appariement maximal égale la taille de la couverture minimale.
Algorithme hongrois : Appariement de coût minimal en O(n³).
Applications : Affectation de tâches, mariages stables.
Techniques avancées pour les gros graphes :
© 2024 - Cours sur les graphes - Niveau Lycée / Supérieur
